| Aceptar H0 | Rechazar H0 | |
|---|---|---|
| H0 es verdadera | Verdadero positivo | Falso negativo |
| H1 es verdadera | Falso positivo | Verdadero negativo |
Poder y tamaño de muestra
Esta versión del capítulo fue traducida de manera automática utilizando IA. El capítulo aún no ha sido revisado por un humano.
Calcular el poder y el tamaño de muestra son tareas comunes en el diseño de estudios. Este capítulo te guiará a través del análisis de poder para estudios de redes. Primero, comenzaremos con algunos preliminares sobre tipos de error y poder estadístico.
Tipos de error
Una de las tablas más importantes que veremos es la tabla de contingencia de aceptar/rechazar la hipótesis nula condicional en el estado verdadero:
Una mejor manera, versión más estadísticamente precisa de esta tabla sería
| Aceptar H0 | Rechazar H0 | |
|---|---|---|
| H0 es verdadera | Inferencia correcta | Error Tipo I |
| H1 es verdadera | Error Tipo II | Inferencia Correcta |
Con \Pr{(\text{Error Tipo I})} = \alpha y \Pr{(\text{Error Tipo II})} = \beta. De esta manera, el poder puede definirse como la probabilidad de rechazar la nula dado que la alternativa es verdadera, \Pr{(\text{Rechazar H0}|\text{H1 es verdadera})} = 1-\beta.
Ejemplo 1: Tamaño de muestra para una proporción
Imaginemos que estamos preparando un estudio en el cual nos gustaría estimar la proporción de individuos con un estado dado. Formalmente, entonces decimos que la variable Y\sim\text{Bernoulli}(p). Para hacerlo, necesitaremos encuestar n individuos y estimar tal número tomando el promedio muestral. Además, hipotetizamos que bajo la nula la proporción es H_0: p = p_0.
La clave aquí es pensar en una regla de rechazo simple. De nuevo, el poder es la probabilidad de rechazar la nula dado que la alternativa es verdadera. Así que, para escribir la ecuación, necesitamos pensar en regiones de aceptación y rechazo. Sea \hat p nuestro estimado para el parámetro poblacional, además, \hat p = n^{-1}\sum_i y_i. Nuestra estadística de prueba puede ser–y será, la mayoría de los casos–estandarizada para aprovechar la ley de los grandes números; bajo la nula, escribimos lo siguiente:
\begin{align*} \mathbb{E}(\hat p) & = p_0 \\ \mathbf{Var}(\hat p) & = \sqrt{p_0(1-p_0)/n} \end{align*}
Por lo tanto, la estadística:
\begin{equation*} \frac{\hat p - p_0}{\sqrt{p_0(1-p_0)/n}} = \frac{\sqrt{n}(\hat p - p_0)}{\sqrt{p_0(1-p_0)}} \sim \text{N}(0, 1) \end{equation*}
Dado que la estadística está distribuida normalmente, podemos entonces decir cuándo rechazaremos la nula. Para este caso, eso depende del valor crítico, que la mayoría de las veces se define en términos de la tasa de error tipo I. Formalmente, rechazamos la nula si
\begin{equation*} \frac{\sqrt{n}(\hat p - p_0)}{\sqrt{p_0(1-p_0)}} > Z_{1-\alpha/2} \end{equation*}
Esto es equivalente a decir que la estadística de prueba cayó en la región de rechazo. Con esto en mano, ahora podemos escribir la ecuación que usaremos para calcular el tamaño de muestra. Volviendo a la definición de poder:
\begin{align*} \Pr{(\text{Rechazar H0}|\text{H1 es verdadera})} & = 1-\beta \\ \Pr{\left(\frac{\sqrt{n}(\hat p - p_0)}{\sqrt{p_0(1-p_0)}} > Z_{1-\alpha/2}\right.\left|\vphantom{\frac{1}{2}}p = p_1\right)} & = 1 - \beta \end{align*}
Observa que no podemos calcular el poder para todo p\neq p_0; en su lugar, vemos un valor de parámetro dado. Una buena idea es empezar desde uno previamente conocido o identificado en otros estudios. La idea clave aquí es poder manipular el argumento de la probabilidad para convertirlo en una distribución conocida, por ejemplo, la distribución normal:
Para un Tipo I dado de 0.05 y poder de 0.8, el tamaño de muestra requerido puede calcularse como sigue:
\begin{align*} 1 - \beta & = \Pr{\left(\frac{\sqrt{n}(\hat p - p_0)}{\sqrt{p_0(1-p_0)}} > Z_{1-\alpha/2}\right.\left|\vphantom{\frac{1}{2}}p = p_1\right)} \\ & = \Pr{\left(\frac{\sqrt{n}(\hat p - p_0)}{\sqrt{p_0(1-p_0)}} < Z_{\alpha/2}\right.\left|\vphantom{\frac{1}{2}}p = p_1\right)} \\ & = \Pr{\left(\frac{\sqrt{n}(\hat p - p_0)}{\sqrt{p_1(1-p_1)}} < \frac{Z_{\alpha/2}\sqrt{p_0(1-p_0)}}{\sqrt{p_1(1-p_1)}}\right.\left|\vphantom{\frac{1}{2}}p = p_1\right)} \\ & = \Pr{\left(\frac{\sqrt{n}(\hat p - p_0 + p_0 - p_1)}{\sqrt{p_1(1-p_1)}} < \frac{Z_{\alpha/2}\sqrt{p_0(1-p_0)} + \sqrt{n}(p_0 - p_1)}{\sqrt{p_1(1-p_1)}}\right.\left|\vphantom{\frac{1}{2}}p = p_1\right)} \\ & = \Pr{\left(\frac{\sqrt{n}(\hat p - p_1)}{\sqrt{p_1(1-p_1)}} < \frac{Z_{\alpha/2}\sqrt{p_0(1-p_0)} + \sqrt{n}(p_0 - p_1)}{\sqrt{p_1(1-p_1)}}\right.\left|\vphantom{\frac{1}{2}}p = p_1\right)} \\ & = \Phi\left(\frac{Z_{\alpha/2}\sqrt{p_0(1-p_0)} + \sqrt{n}(p_0 - p_1)}{\sqrt{p_1(1-p_1)}}\right.\left|\vphantom{\frac{1}{2}}p = p_1\right) \\ \end{align*}
La última igualdad sigue de la cantidad \frac{\sqrt{n}(\hat p - p_1)}{\sqrt{p_1(1-p_1)}} distribuyendo normal estándar. Ahora podemos tomar la inversa de la función de distribución acumulativa (cdf) para aislar el tamaño de muestra n:
\begin{align*} \Phi^{-1}(1 - \beta)& = \frac{Z_{\alpha/2}\sqrt{p_0(1-p_0)} + \sqrt{n}(p_0 - p_1)}{\sqrt{p_1(1-p_1)}} \\ Z_{1-\beta}\sqrt{p_1(1-p_1)}& = Z_{\alpha/2}\sqrt{p_0(1-p_0)} + \sqrt{n}(p_0 - p_1) \\ \frac{\left(Z_{1-\beta}\sqrt{p_1(1-p_1)} - Z_{\alpha/2}\sqrt{p_0(1-p_0)}\right)^2}{(p_0 - p_1)^2}& = n \\ \end{align*}
Por lo tanto, para los parámetros (1-\beta, \alpha, p_0, p_1) = (0.8, 0.05, 0.5, 0.6), el tamaño de muestra requerido es 193.8473 \sim 194.
Ejemplo 2: Tamaño de muestra para una proporción (vis)
Ahora, ¿qué pasa si el modelo que estamos planeando estimar no tiene una forma cerrada? Si las soluciones analíticas no están disponibles, las simulaciones pueden ser una excelente alternativa para salvar el día. Rehagamos el cálculo de tamaño de muestra usando simulaciones.
El procedimiento para calcular el tamaño de muestra basado en simulaciones es computacionalmente intensivo. El concepto es directo, escoger un conjunto de mejores conjeturas para el tamaño de muestra, y para cada una de ellas, simular el sistema para estimar el poder. Ahora, para un valor dado de n, nosotros:
Simulamos una muestra de tamaño n bajo la alternativa.
Calculamos la estadística de prueba correspondiente a la nula.
Aceptamos o rechazamos de acuerdo al \alpha seleccionado, y almacenamos el resultado.
Repetimos los pasos 1-3 muchas veces. El promedio obtenido es el poder correspondiente.
Cuando ejecutamos simulaciones, es conveniente escribir una función para el proceso de generación de datos. En nuestro caso, la función se llamará sim_fun. Las siguientes líneas de código logran nuestro objetivo: aproximar el poder simulando 10,000 experimentos para cada candidato de tamaño de muestra:
# Parámetros del modelo
p0 <- .5
p1 <- .6
betapower <- 1 - 0.8
alpha <- 0.05
nsims <- 10000
# Paso 1: Simular los datos bajo H1
z_one_minus_alpha_half <- qnorm(1 - alpha / 2)
sim_fun <- function(n) {
# Generando los datos
y <- as.integer(runif(n) < p1)
phat <- mean(y)
# ¿Aceptar o rechazar?
sqrt(n) * (phat - p0) / sqrt(p0 * (1 - p0)) >
z_one_minus_alpha_half
}
# Paso 2: Para un arreglo de n, simular múltiples experimentos
n_seq <- seq(from = 150, to = 250, by = 10)
simulations <- NULL
set.seed(12312)
for (n in n_seq) {
# Ejecutar los nsims experimentos
res <- replicate(nsims, sim_fun(n))
# Calcular poder y almacenar el valor
simulations <- rbind(
simulations,
data.frame(size = n, power = mean(res))
)
}
# Descubriendo cuál es el valor más cercano
best <- which.min(
abs((1 - betapower) - simulations$power)
)
simulations[best,,drop=FALSE] size power
5 190 0.7952Visualicemos la curva de poder que generamos de esta simulación:
library(ggplot2)
ggplot(simulations, aes(x = size, y = power)) +
geom_point() +
geom_smooth() +
geom_hline(yintercept = 1 - betapower)`geom_smooth()` using method = 'loess' and formula = 'y ~ x'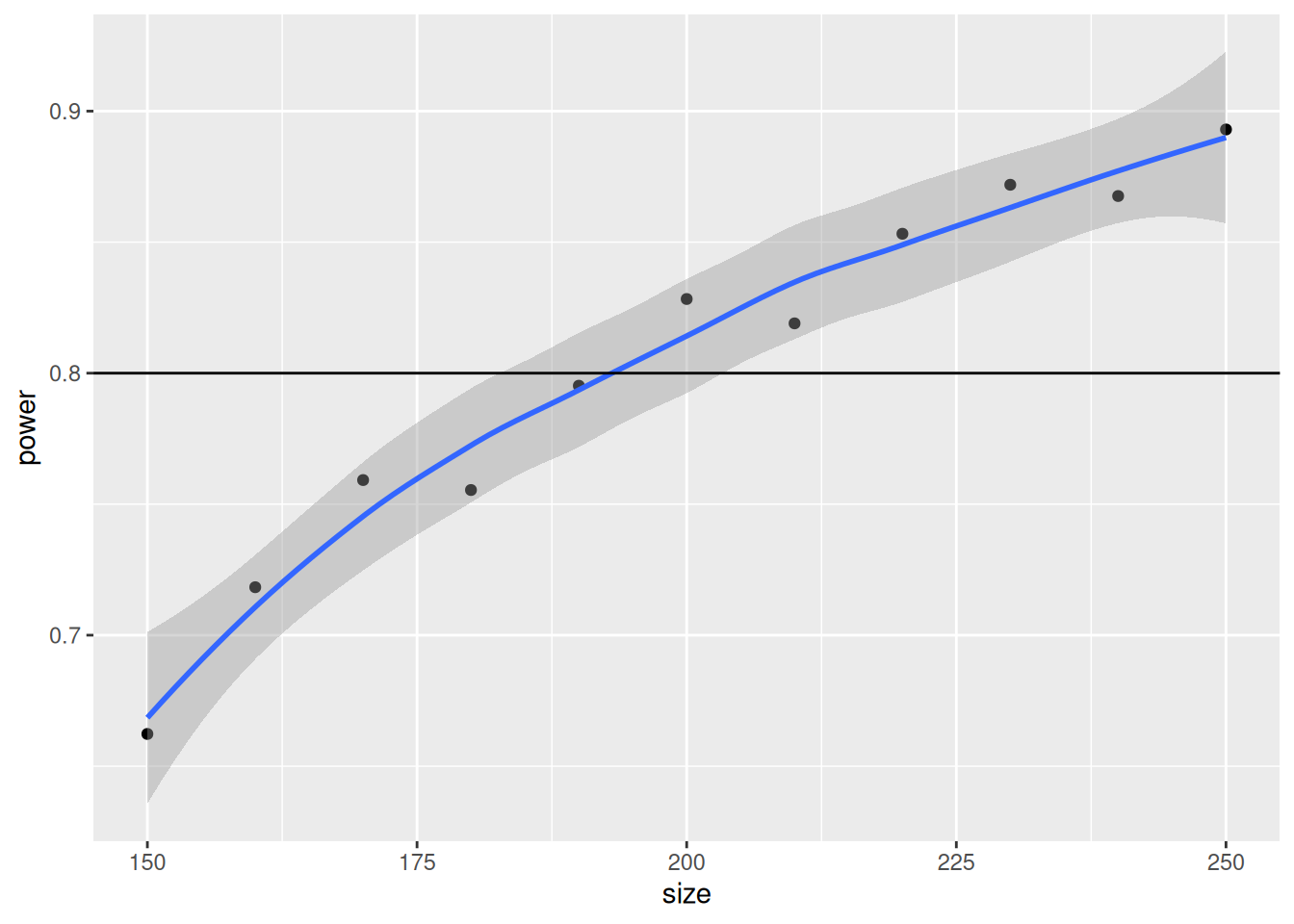
Alternativamente, podemos ajustar un modelo de regresión lineal donde predecimos el poder como una función del tamaño de muestra usando efectos lineales y cuadráticos:
n = \theta_0 + \theta_1 (1 - \beta) + \theta_2 (1 - \beta)^2
# Ajustando el modelo
power_model <- glm(
size ~ power + I(power^2),
data = simulations, family = gaussian()
)
# Imprimiendo los resultados
summary(power_model)
Call:
glm(formula = size ~ power + I(power^2), family = gaussian(),
data = simulations)
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 632.5 232.9 2.715 0.02644 *
power -1590.3 598.1 -2.659 0.02885 *
I(power^2) 1301.0 381.6 3.410 0.00923 **
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Dispersion parameter for gaussian family taken to be 34.83159)
Null deviance: 11000.00 on 10 degrees of freedom
Residual deviance: 278.65 on 8 degrees of freedom
AIC: 74.769
Number of Fisher Scoring iterations: 2# Predecir
predict(power_model, newdata = data.frame(power = .8), type = "response") |>
ceiling() 1
193 Según nuestro estudio de simulación, el más cercano a nuestro 80% de poder es usar un tamaño de muestra igual a 193, que está muy cerca de la solución analítica de 194.
Como comentario final para este ejemplo, recuerda que mientras más simulaciones mejor.