Modelos Exponenciales de Grafos Aleatorios

Published

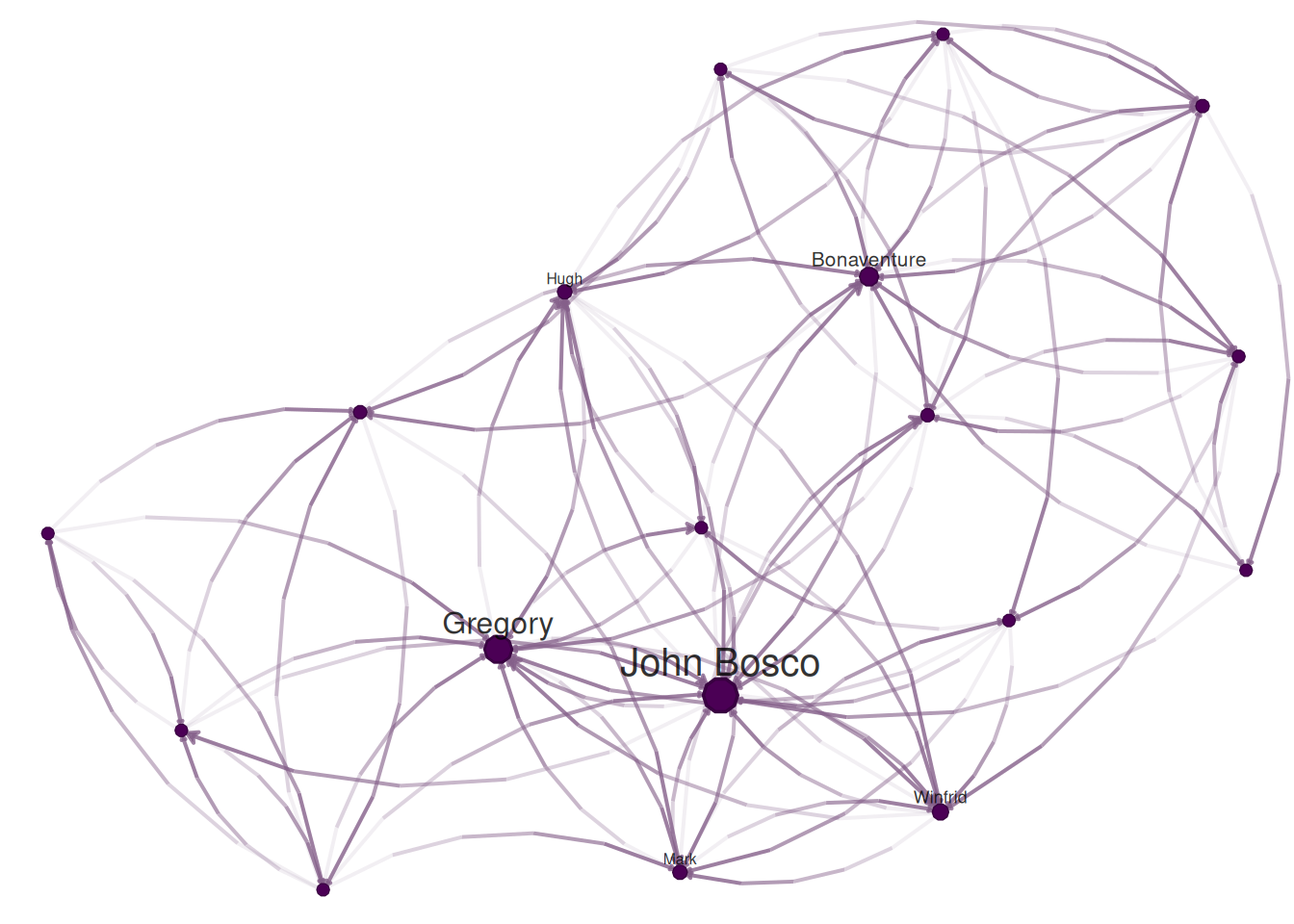
June 27, 2024

Modified

September 3, 2025

Recomiendo encarecidamente leer la viñeta del paquete de R ergm.

vignette("ergm", package="ergm")

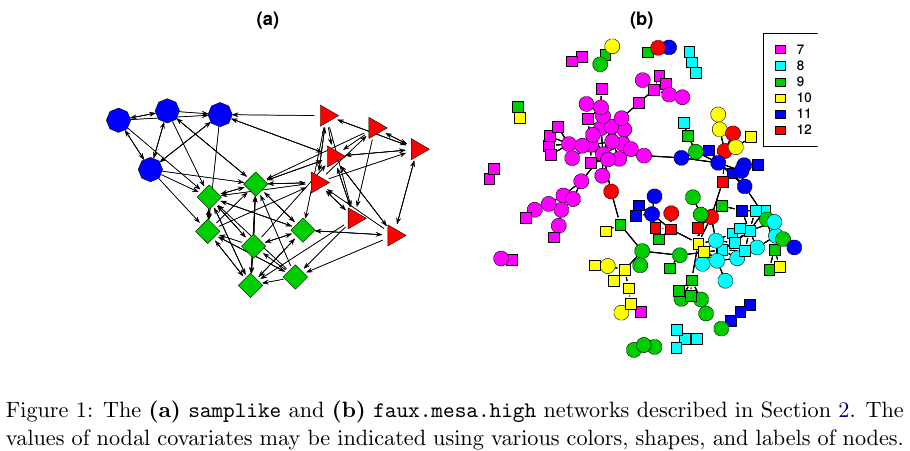
El propósito de los ERGMs, en pocas palabras, es describir de manera parsimoniosa las fuerzas de selección local que dan forma a la estructura global de una red. Para este fin, un conjunto de datos de red, como los que se muestran en la Figura 1, puede ser considerado como la respuesta en un modelo de regresión, donde los predictores son cosas como “propensión de individuos del mismo sexo a formar asociaciones” o “propensión de individuos a formar triángulos de asociaciones”. En la Figura 1(b), por ejemplo, es evidente que los nodos individuales parecen agruparse en grupos de las mismas etiquetas numéricas (que resultan ser las calificaciones de los estudiantes, del 7 al 12); por lo tanto, un ERGM puede ayudarnos a cuantificar la fuerza de este efecto intra-grupo.

— (David R. Hunter et al. 2008)

Fuente: Hunter et al. (2008)

En pocas palabras, usamos ERGMs (que en inglés son “Exponential Random Graph Models”) como una interpretación paramétrica de la distribución de \mathbf{Y}, que toma la forma canónica:

{\mathbb{P}_{\mathcal{Y}}\left(\mathbf{Y}=\mathbf{y};\mathbf{\theta}\right) } = \frac{\text{exp}\left\{\theta^{\text{T}}\mathbf{g}(\mathbf{y})\right\}}{\kappa\left(\theta, \mathcal{Y}\right)},\quad\mathbf{y}\in\mathcal{Y} \tag{9.1}

Donde \theta\in\Omega\subset\mathbb{R}^q es el vector de coeficientes del modelo y \mathbf{g}(\mathbf{y}) es un q-vector de estadísticas basadas en la matriz de adyacencia \mathbf{y}.

El modelo Equation 9.1 puede expandirse reemplazando \mathbf{g}(\mathbf{y}) con \mathbf{g}(\mathbf{y}, \mathbf{X}) para permitir información adicional de covariables \mathbf{X} sobre la red. El denominador \kappa\left(\theta,\mathcal{Y}\right) = \sum_{\mathbf{y}\in\mathcal{Y}}\text{exp}\left\{\theta^{\text{T}}\mathbf{g}(\mathbf{y})\right\} es el factor normalizador que asegura que la ecuación Equation 9.1 sea una distribución de probabilidad legítima. Incluso después de fijar \mathcal{Y} para que sean todas las redes que tienen tamaño n, el tamaño de \mathcal{Y} hace que este tipo de modelo estadístico sea difícil de estimar ya que hay N = 2^{n(n-1)} redes posibles! (David R. Hunter et al. 2008)

Desarrollos posteriores incluyen nuevas estructuras de dependencia para considerar efectos de vecindario más generales. Estos modelos relajan las suposiciones de dependencia markoviana de un paso, permitiendo la investigación de configuraciones de mayor alcance, como rutas más largas en la red o ciclos más grandes (Pattison y Robins 2002). Se han desarrollado modelos para estructuras de red bipartitas (Faust y Skvoretz 1999) y tripartitas (Mische y Robins 2000). (David R. Hunter et al. 2008, 9)

Un ejemplo ingenuo

En el caso más simple, los ERGMs equivalen a una regresión logística. Por simple, me refiero a casos sin términos markovianos–motivos que involucran más de un enlace–por ejemplo, el grafo de Bernoulli. En el grafo de Bernoulli, los vínculos son independientes, por lo que la presencia/ausencia de un vínculo entre los nodos i y j no afectará la presencia/ausencia de un vínculo entre los nodos k y l.

Ajustemos un ERGM usando el conjunto de datos sampson en el paquete ergm.

library(ergm)
library(netplot)
data("sampson")
nplot(samplike)

Usar ergm para ajustar un grafo de Bernoulli requiere usar el término edges, que cuenta cuántos vínculos hay en el grafo:

ergm_fit <- ergm(samplike ~ edges)
## Starting maximum pseudolikelihood estimation (MPLE):
## Obtaining the responsible dyads.
## Evaluating the predictor and response matrix.
## Maximizing the pseudolikelihood.
## Finished MPLE.
## Evaluating log-likelihood at the estimate.

Dado que esto es equivalente a una regresión logística, podemos usar la función glm para ajustar el mismo modelo. Primero, necesitamos preparar los datos para que podamos pasarlos a glm:

y <- sort(as.vector(as.matrix(samplike)))
y <- y[-c(1:18)] # Eliminamos la diagonal del modelo, que es todo 0.
y
##   [1] 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
##  [38] 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
##  [75] 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
## [112] 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
## [149] 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
## [186] 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1
## [223] 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
## [260] 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
## [297] 1 1 1 1 1 1 1 1 1 1

Ahora podemos ajustar el modelo GLM:

glm_fit <- glm(y~1, family=binomial("logit"))

Los coeficientes de ambos ERGM y GLM deberían coincidir:

glm_fit
## 
## Call:  glm(formula = y ~ 1, family = binomial("logit"))
## 
## Coefficients:
## (Intercept)  
##     -0.9072  
## 
## Degrees of Freedom: 305 Total (i.e. Null);  305 Residual
## Null Deviance:       367.2 
## Residual Deviance: 367.2     AIC: 369.2
ergm_fit
## 
## Call:
## ergm(formula = samplike ~ edges)
## 
## Maximum Likelihood Coefficients:
##   edges  
## -0.9072

Además, en el caso del grafo de Bernoulli, podemos obtener la estimación usando la función Logit:

pr <- mean(y)
# Función Logit:
# Alternativamente podríamos haber usado log(pr) - log(1-pr)
qlogis(pr)
## [1] -0.9071582

De nuevo, el mismo resultado. El grafo de Bernoulli no es el único modelo ERGM que puede ajustarse usando una regresión logística. Además, si todos los términos del modelo son términos no-Markov, ergm automáticamente usa por defecto una regresión logística.

Estimación de ERGMs

El objetivo final es realizar inferencia estadística sobre el modelo propuesto. En un entorno estándar, podríamos usar Estimación de Máxima Verosimilitud (MLE, por sus siglas en inglés), que consiste en encontrar los parámetros del modelo \theta que, dados los datos observados, maximicen la verosimilitud del modelo. Para esto último, generalmente usamos el método de Newton. El método de Newton requiere calcular la log-verosimilitud del modelo, lo que puede ser desafiante en ERGMs.

Para ERGMs, dado que parte de la verosimilitud involucra una constante normalizadora que es una función de todas las redes posibles, esto no es tan directo como en el entorno regular. Debido a esto, la mayoría de los métodos de estimación se basan en simulaciones.

En statnet, el método de estimación predeterminado se basa en un método propuesto por (Geyer and Thompson 1992), MLE de Cadena de Markov, que usa Monte Carlo de Cadena de Markov para simular redes y una versión modificada del algoritmo Newton-Raphson para estimar los parámetros.

La idea del MC-MLE para esta familia de modelos estadísticos es aproximar la expectativa de las razones de constantes normalizadoras usando la ley de los grandes números. En particular, lo siguiente:

\begin{align*} \frac{\kappa\left(\theta,\mathcal{Y}\right)}{\kappa\left(\theta_0,\mathcal{Y}\right)} & = \frac{ \sum_{\mathbf{y}\in\mathcal{Y}}\text{exp}\left\{\theta^{\text{T}}\mathbf{g}(\mathbf{y})\right\}}{ \sum_{\mathbf{y}\in\mathcal{Y}}\text{exp}\left\{\theta_0^{\text{T}}\mathbf{g}(\mathbf{y})\right\} } \\ & = \sum_{\mathbf{y}\in\mathcal{Y}}\left( % \frac{1}{% \sum_{\mathbf{y}\in\mathcal{Y}\text{exp}\left\{\theta_0^{\text{T}}\mathbf{g}(\mathbf{y})\right\}}% } \times % \text{exp}\left\{\theta^{\text{T}}\mathbf{g}(\mathbf{y})\right\} % \right) \\ & = \sum_{\mathbf{y}\in\mathcal{Y}}\left( % \frac{\text{exp}\left\{\theta_0^{\text{T}}\mathbf{g}(\mathbf{y})\right\}}{% \sum_{\mathbf{y}\in\mathcal{Y}\text{exp}\left\{\theta_0^{\text{T}}\mathbf{g}(\mathbf{y})\right\}}% } \times % \text{exp}\left\{(\theta - \theta_0)^{\text{T}}\mathbf{g}(\mathbf{y})\right\} % \right) \\ & = \sum_{\mathbf{y}\in\mathcal{Y}}\left( % {\mathbb{P}_{\times }\left(Y = y|\mathcal{Y}, \theta_0\right) }% \text{exp}\left\{(\theta - \theta_0)^{\text{T}}\mathbf{g}(\mathbf{y})\right\} % \right) \\ & = \text{E}_{\theta_0}\left(\text{exp}\left\{(\theta - \theta_0)^{\text{T}}\mathbf{g}(\mathbf{y})\right\} \right) \end{align*}

En particular, el algoritmo MC-MLE usa este hecho para maximizar la razón de log-verosimilitud. La función objetivo misma puede aproximarse simulando m redes de la distribución con parámetro \theta_0:

l(\theta) - l(\theta_0) \approx (\theta - \theta_0)^{\text{T}}\mathbf{g}(\mathbf{y}_{obs}) - \text{log}{\left[\frac{1}{m}\sum_{i = 1}^m\text{exp}\left\{(\theta-\theta_0)^{\text{T}}\right\}\mathbf{g}(\mathbf{Y}_i)\right]}

Para más detalles, ver (David R. Hunter et al. 2008). Un bosquejo del algoritmo sigue:

  1. Inicializar el algoritmo con una conjetura inicial de \theta, llamarlo \theta^{(t)} (debe ser una conjetura bastante buena)

  2. Mientras (no haya convergencia) hacer:

  1. Usando \theta^{(t)}, simular M redes por medio de pequeños cambios en la \mathbf{Y}_{obs} (la red observada). Esta parte se hace usando un método de muestreo de importancia que pondera cada red propuesta por su verosimilitud condicional en \theta^{(t)}

  2. Con las redes simuladas, podemos hacer el paso de Newton para actualizar el parámetro \theta^{(t)} (esta es la parte de iteración en el paquete ergm): \theta^{(t)}\to\theta^{(t+1)}.

  3. Si se ha alcanzado la convergencia (lo que usualmente significa que \theta^{(t)} y \theta^{(t + 1)} no son muy diferentes), entonces parar; de lo contrario, ir al paso a.

Lusher, Koskinen, and Robins (2013);Admiraal and Handcock (2006);Snijders (2002);Wang et al. (2009) proporcionan detalles sobre el algoritmo usado por PNet (el mismo que el usado en RSiena), y Lusher, Koskinen, and Robins (2013) proporciona una breve discusión sobre las diferencias entre ergm y PNet.

El paquete ergm

De la sección anterior:1

library(igraph)

library(dplyr)

load("03.rda")

En esta sección, usaremos el paquete ergm (del conjunto de paquetes statnet Handcock et al. (2023),) y el paquete intergraph (Bojanowski 2023). Este último proporciona funciones para ir y venir entre objetos igraph y network de los paquetes igraph y network respectivamente2

library(ergm)
library(intergraph)

Como una nota lateral bastante importante, el orden en que se cargan los paquetes de R importa. ¿Por qué es importante mencionarlo ahora? Bueno, resulta que al menos un par de funciones en el paquete network tienen el mismo nombre que algunas funciones en el paquete igraph. Cuando se carga el paquete ergm, dado que depende de network, cargará el paquete network primero, lo que enmascarará algunas funciones en igraph. Esto se vuelve evidente una vez que cargas ergm después de cargar igraph:

Los siguientes objetos están enmascarados desde 'package:igraph':

  add.edges, add.vertices, %c%, delete.edges, delete.vertices, get.edge.attribute, get.edges,
  get.vertex.attribute, is.bipartite, is.directed, list.edge.attributes, list.vertex.attributes, %s%,
  set.edge.attribute, set.vertex.attribute

¿Cuáles son las implicaciones de esto? Si llamas la función list.edge.attributes para un objeto de clase igraph R devolverá un error ya que la primera función que coincide con ese nombre viene del paquete network! Para evitar esto puedes usar la notación de doble dos puntos:

igraph::list.edge.attributes(my_igraph_object)
network::list.edge.attributes(my_network_object)

Usando la función asNetwork, podemos coercionar el objeto igraph en un objeto network para que podamos usarlo con la función ergm:

# Creando la nueva red
network_111 <- intergraph::asNetwork(ig_year1_111)

# Ejecutando un ergm simple (solo ajustando cuenta de enlaces)
ergm(network_111 ~ edges)
## Warning in ergm.getnetwork(formula): This network contains loops
## Starting maximum pseudolikelihood estimation (MPLE):
## Obtaining the responsible dyads.
## Evaluating the predictor and response matrix.
## Maximizing the pseudolikelihood.
## Finished MPLE.
## Evaluating log-likelihood at the estimate.
## 
## Call:
## ergm(formula = network_111 ~ edges)
## 
## Maximum Likelihood Coefficients:
##  edges  
## -4.734

Entonces, ¿qué pasó aquí? Obtuvimos una advertencia. Resulta que nuestra red tiene bucles (¡no pensé en eso antes!), que son arcos que conectan un nodo consigo mismo. Echemos un vistazo a eso con la función which_loop

E(ig_year1_111)[which_loop(ig_year1_111)]
## + 1/2638 edge from acc1127 (vertex names):
## [1] 1110111->1110111

Podemos deshacernos de estos usando el igraph::-.igraph. Eliminemos los aislados usando el mismo operador

# Creando la nueva red
network_111 <- ig_year1_111

# Eliminando bucles
network_111 <- network_111 - E(network_111)[which(which_loop(network_111))]

# Eliminando aislados
network_111 <- network_111 - which(degree(network_111, mode = "all") == 0)

# Convirtiendo la red
network_111 <- intergraph::asNetwork(network_111)

asNetwork(simplify(ig_year1_111)) ig_year1_111 |> simplify() |> asNetwork()

Un problema que tenemos con estos datos es el hecho de que algunos vértices tienen valores faltantes en las variables hispanic, female1, y eversmk1. Por ahora, procederemos imputando valores basados en los promedios:

for (v in c("hispanic", "female1", "eversmk1")) {
  tmpv <- network_111 %v% v
  tmpv[is.na(tmpv)] <- mean(tmpv, na.rm = TRUE) > .5
  network_111 %v% v <- tmpv
}

Echemos un vistazo a la red

nplot(
  network_111,
  vertex.color = ~ hispanic
  )
Figure 9.1

Colorando por hispanic, podemos ver que los nodos parecen estar agrupados por este atributo. La inspección visual en la ciencia de redes puede ser muy útil, pero, para hacer declaraciones más formales, necesitamos usar modelos estadísticos; aquí es donde los ERGMs brillan.

Estimando ERGMs

Aunque no existe una solución única para estimar estos modelos, el siguiente flujo de trabajo me ha funcionado en el pasado:

  1. Estimar el modelo más simple, agregando una variable a la vez.

  2. Después de cada estimación, ejecutar la función mcmc.diagnostics para ver qué tan bien (o mal) se comportaron las cadenas.

  3. Ejecutar la función gof y verificar qué tan bien el modelo coincide con las estadísticas estructurales de la red.

Qué usar:

  1. control.ergms: Número máximo de iteraciones, semilla para Pseudo-RNG, cuántos núcleos

  2. ergm.constraints: De dónde muestrear la red. Da estabilidad y (en algunos casos) convergencia más rápida ya que al restringir el modelo estás reduciendo el tamaño de la muestra.

Aquí hay un ejemplo de un par de modelos que podríamos comparar

Note

Nota que este documento puede no incluir los mensajes usuales que el comando ergm genera durante el procedimiento de estimación. Esto es solo para hacerlo más amigable para imprimir.

ans0 <- ergm(
  network_111 ~
    edges +
    nodematch("hispanic") +
    nodematch("female1") +
    nodematch("eversmk1") +
    mutual,
  control = control.ergm(
    seed        = 1,
    MCMLE.maxit = 10,
    parallel    = 4,
    CD.maxit    = 10
    )
  )
## Warning: 'glpk' selected as the solver, but package 'Rglpk' is not available;
## falling back to 'lpSolveAPI'. This should be fine unless the sample size and/or
## the number of parameters is very big.
Versión anterior del libro

En una versión anterior del libro usamos la restricción bd para limitar el número máximo de vínculos salientes a 19. Aunque esta es una restricción razonable (ya que la muestra pudo haber sido restringida por construcción), la versión actual del paquete ERGM devuelve una advertencia y muestra las estadísticas GOF con signos cambiados (AIC y BIC negativos, y Logverosimilitud positiva).

Entonces, ¿qué estamos haciendo aquí:

  1. El modelo está controlando por:

    1. edges Número de enlaces en la red (en oposición a su densidad)

    2. nodematch("algún-nombre-de-variable-aquí") Incluye un término que controla por homofilia/heterofilia

    3. mutual Número de conexiones mutuas entre (i, j), (j, i). Esto puede estar relacionado con, por ejemplo, cierre triádico.

Para más sobre parámetros de control, ver Morris, Handcock, and Hunter (2008). El siguiente modelo consiste en una version más simple del modelo anterior. Excluye el término mutual lleva a un modelo sin términos markovianos, es decir, los estadísticos de la red son funciones de enlaces individuales y no de pares de enlaces o más. El término mutual incluye dos enlaces (i\to j y j\to i). Modelos sin términos markovianos pueden ser estimados usando regresión logística, evitando la necesidad de simulaciones MCMC:

ans1 <- ergm(
  network_111 ~
    edges +
    nodematch("hispanic") +
    nodematch("female1") +
    nodematch("eversmk1")
    ,
  control = control.ergm(
    seed        = 1,
    MCMLE.maxit = 10,
    parallel    = 4,
    CD.maxit    = 10
    )
  )

Finalmente, podemos intentar estimar un modelo con términos más complejos, por ejemplo, el geometrically weighted edge-wise shared partner (gwesp). Éste término captura el cierre triádico, pero es más fácil de estimar que triangle. Más aún, para facilitar el proceso de estimación, podemos incorporar el termino geometrically weighted dyad-wise shared partner (gwdsp). Ambos estadísticos incluyen un parámetro de descuento (decay); por el momento, fijaremos ambos parametros en 0.5 (valores entre 0.25 y 1.5 son comunes). Más detalles sobre estos términos en David R. Hunter (2007).

ans2 <- ergm(
  network_111 ~
    edges +
    nodematch("hispanic") +
    nodematch("female1") +
    nodematch("eversmk1") + 
    mutual +
    gwesp(decay = 0.5, fixed = TRUE) +
    gwdsp(decay = 0.5, fixed = TRUE)
    ,
  control = control.ergm(
    seed        = 1,
    MCMLE.maxit = 10,
    parallel    = 4,
    CD.maxit    = 10
    )
  )

Ahora, un truco agradable para ver todas las regresiones en la misma tabla, podemos usar el paquete texreg (Leifeld 2013) que soporta salidas de ergm!

library(texreg)
## Version:  1.39.4
## Date:     2024-07-23
## Author:   Philip Leifeld (University of Manchester)
## 
## Consider submitting praise using the praise or praise_interactive functions.
## Please cite the JSS article in your publications -- see citation("texreg").
screenreg(list(ans0, ans1, ans2))
## 
## ================================================================
##                      Model 1        Model 2        Model 3      
## ----------------------------------------------------------------
## edges                    -5.62 ***      -5.49 ***      -4.73 ***
##                          (0.05)         (0.06)         (0.07)   
## nodematch.hispanic        0.22 ***       0.30 ***       0.16 ***
##                          (0.04)         (0.05)         (0.03)   
## nodematch.female1         0.87 ***       1.16 ***       0.47 ***
##                          (0.04)         (0.05)         (0.03)   
## nodematch.eversmk1        0.33 ***       0.45 ***       0.23 ***
##                          (0.04)         (0.04)         (0.03)   
## mutual                    4.10 ***                      2.72 ***
##                          (0.07)                        (0.08)   
## gwesp.OTP.fixed.0.5                                     1.34 ***
##                                                        (0.03)   
## gwdsp.OTP.fixed.0.5                                    -0.11 ***
##                                                        (0.01)   
## ----------------------------------------------------------------
## AIC                   22649.55       25135.63       20155.83    
## BIC                   22699.89       25175.91       20226.31    
## Log Likelihood       -11319.77      -12563.82      -10070.91    
## ================================================================
## *** p < 0.001; ** p < 0.01; * p < 0.05

O, si estás usando rmarkdown, puedes exportar los resultados usando LaTeX o html, intentemos este último para ver cómo se ve aquí:

library(texreg)
htmlreg(list(ans0, ans1, ans2))
Statistical models
  Model 1 Model 2 Model 3
edges -5.62*** -5.49*** -4.73***
  (0.05) (0.06) (0.07)
nodematch.hispanic 0.22*** 0.30*** 0.16***
  (0.04) (0.05) (0.03)
nodematch.female1 0.87*** 1.16*** 0.47***
  (0.04) (0.05) (0.03)
nodematch.eversmk1 0.33*** 0.45*** 0.23***
  (0.04) (0.04) (0.03)
mutual 4.10***   2.72***
  (0.07)   (0.08)
gwesp.OTP.fixed.0.5     1.34***
      (0.03)
gwdsp.OTP.fixed.0.5     -0.11***
      (0.01)
AIC 22649.55 25135.63 20155.83
BIC 22699.89 25175.91 20226.31
Log Likelihood -11319.77 -12563.82 -10070.91
***p < 0.001; **p < 0.01; *p < 0.05

En base a los resultados, podemos hacer las siguientes observaciones:

  1. De los tres modelos, el último es el mejor en términos de menor AIC y BIC, y mayor Logverosimilitud.

  2. Todos los términos nodematch son significativos y positivos, lo que significa que tenemos homofilia por hispanic, female1, y eversmk1.

  3. El término mutual es significativo, positivo y grande (~4). Esto indica una fuerte tendencia de los individuos a establecer amistad mutua.

  4. El término gwesp es positivo y significativo. La interpretación de este término no siempre es simple. Generalmente, decimos que un término gwesp positivo significa que hay una tendencia hacia el cierre triádico.

Bondad de Ajuste del Modelo

En términos brutos, una vez que cada cadena ha alcanzado la distribución estacionaria, podemos decir que no hay problemas con la autocorrelación y que cada punto de muestra es iid. Esto último implica que, dado que estamos ejecutando el modelo con más de una cadena, podemos usar todas las muestras (cadenas) como un solo conjunto de datos.

Cambios recientes en el algoritmo de estimación de ergm significan que estos gráficos ya no pueden usarse para asegurar que las estadísticas medias del modelo coincidan con las estadísticas de red observadas. Para esa funcionalidad, por favor usa el comando GOF: gof(object, GOF=~model).

—?ergm::mcmc.diagnostics

Dado que ans2 es el mejor modelo, veamos las estadísticas GOF. Primero, veamos cómo se comportó el MCMC. Podemos usar la función mcmc.diagnostics incluida en el paquete. La función es un envoltorio de un par de funciones del paquete coda (Plummer et al. 2006), que son llamadas sobre el objeto $sample que contiene las estadísticas centradas de las redes muestreadas. Al principio, puede ser confuso mirar el objeto $sample; no coincide ni con las estadísticas observadas ni con los coeficientes.

Cuando se llama mcmc.diagnostics(ans2, centered = FALSE), verás muchas salidas, incluyendo un par de gráficos mostrando la traza y distribución posterior de las estadísticas no centradas (centered = FALSE). Los siguientes fragmentos de código reproducirán la salida de la función mcmc.diagnostics paso a paso usando el paquete coda. Primero, necesitamos descentrar el objeto de muestra:

# Obteniendo la muestra centrada
sample_centered <- ans2$sample

# Obteniendo las estadísticas observadas y convirtiéndolas en una matriz para que podamos agregarlas
# a las muestras
observed <- summary(ans2$formula)
observed <- matrix(
  observed,
  nrow  = nrow(sample_centered[[1]]),
  ncol  = length(observed),
  byrow = TRUE
  )

# Ahora descentramos la muestra
sample_uncentered <- lapply(sample_centered, function(x) {
  x + observed
})

# Tenemos que hacer de esto un objeto mcmc.list
sample_uncentered <- coda::mcmc.list(sample_uncentered)

Bajo el capó:

  1. Medias empíricas y sd, y cuantiles:
summary(sample_uncentered)
## 
## Iterations = 327680:5963776
## Thinning interval = 32768 
## Number of chains = 4 
## Sample size per chain = 173 
## 
## 1. Empirical mean and standard deviation for each variable,
##    plus standard error of the mean:
## 
##                        Mean     SD Naive SE Time-series SE
## edges                2471.9  63.94    2.430          6.221
## nodematch.hispanic   1829.8  59.02    2.244          7.099
## nodematch.female1    1874.4  71.09    2.703          8.346
## nodematch.eversmk1   1755.6  58.02    2.206          6.746
## mutual                481.9  27.72    1.054          3.379
## gwesp.OTP.fixed.0.5  1762.6 113.98    4.333         13.574
## gwdsp.OTP.fixed.0.5 13175.1 644.91   24.516         66.387
## 
## 2. Quantiles for each variable:
## 
##                        2.5%   25%   50%   75% 97.5%
## edges                2347.3  2431  2469  2510  2605
## nodematch.hispanic   1718.3  1791  1827  1867  1955
## nodematch.female1    1736.0  1827  1871  1928  2016
## nodematch.eversmk1   1654.3  1714  1752  1794  1879
## mutual                429.3   462   481   500   542
## gwesp.OTP.fixed.0.5  1540.9  1684  1760  1835  2013
## gwdsp.OTP.fixed.0.5 11958.3 12737 13137 13596 14488
  1. Correlación cruzada:
coda::crosscorr(sample_uncentered)
##                         edges nodematch.hispanic nodematch.female1
## edges               1.0000000          0.8566830         0.8770210
## nodematch.hispanic  0.8566830          1.0000000         0.7573169
## nodematch.female1   0.8770210          0.7573169         1.0000000
## nodematch.eversmk1  0.8229030          0.6949758         0.7455362
## mutual              0.7921269          0.7019044         0.7765035
## gwesp.OTP.fixed.0.5 0.8782943          0.7780147         0.8679069
## gwdsp.OTP.fixed.0.5 0.9678268          0.8370254         0.8591945
##                     nodematch.eversmk1    mutual gwesp.OTP.fixed.0.5
## edges                        0.8229030 0.7921269           0.8782943
## nodematch.hispanic           0.6949758 0.7019044           0.7780147
## nodematch.female1            0.7455362 0.7765035           0.8679069
## nodematch.eversmk1           1.0000000 0.7067807           0.7820246
## mutual                       0.7067807 1.0000000           0.8954091
## gwesp.OTP.fixed.0.5          0.7820246 0.8954091           1.0000000
## gwdsp.OTP.fixed.0.5          0.8098323 0.7688635           0.8575789
##                     gwdsp.OTP.fixed.0.5
## edges                         0.9678268
## nodematch.hispanic            0.8370254
## nodematch.female1             0.8591945
## nodematch.eversmk1            0.8098323
## mutual                        0.7688635
## gwesp.OTP.fixed.0.5           0.8575789
## gwdsp.OTP.fixed.0.5           1.0000000
  1. Autocorrelación: Por ahora, solo veremos la autocorrelación para la cadena uno. La autocorrelación debería ser pequeña (en un entorno MCMC general). Si la autocorrelación es alta, entonces significa que tu muestra no es idd (no hay propiedad de Markov). Una forma de resolver esto es adelgazar la muestra.
coda::autocorr(sample_uncentered)[[1]]
## , , edges
## 
##                   edges nodematch.hispanic nodematch.female1 nodematch.eversmk1
## Lag 0       1.000000000         0.85174677        0.90035143         0.84731435
## Lag 32768   0.604509897         0.52958876        0.66467595         0.54146395
## Lag 163840  0.369212891         0.35412936        0.40011462         0.39283115
## Lag 327680  0.184463035         0.14706318        0.24305479         0.29114538
## Lag 1638400 0.009007472        -0.02631294        0.03456016        -0.04578478
##                 mutual gwesp.OTP.fixed.0.5 gwdsp.OTP.fixed.0.5
## Lag 0       0.83296982           0.9136663          0.97089215
## Lag 32768   0.68928494           0.6870541          0.57938173
## Lag 163840  0.45203629           0.4511364          0.36536136
## Lag 327680  0.12747154           0.1829741          0.15036241
## Lag 1638400 0.05607638           0.0292786         -0.01022981
## 
## , , nodematch.hispanic
## 
##                   edges nodematch.hispanic nodematch.female1 nodematch.eversmk1
## Lag 0       0.851746774         1.00000000       0.796948280         0.77244980
## Lag 32768   0.540210932         0.64168452       0.620791472         0.51899205
## Lag 163840  0.348421398         0.40142712       0.409478507         0.40705581
## Lag 327680  0.156894106         0.10147048       0.226595532         0.24435622
## Lag 1638400 0.007637041        -0.04655592      -0.007443898        -0.07226516
##                 mutual gwesp.OTP.fixed.0.5 gwdsp.OTP.fixed.0.5
## Lag 0       0.69025542         0.795564260          0.82655175
## Lag 32768   0.58418987         0.623959752          0.52242442
## Lag 163840  0.42435250         0.432709863          0.35047668
## Lag 327680  0.11948613         0.174673754          0.13223947
## Lag 1638400 0.05123385         0.007771714         -0.02509792
## 
## , , nodematch.female1
## 
##                  edges nodematch.hispanic nodematch.female1 nodematch.eversmk1
## Lag 0       0.90035143        0.796948280        1.00000000         0.79308088
## Lag 32768   0.60258009        0.536790742        0.73348572         0.56527326
## Lag 163840  0.32695326        0.324827911        0.37903351         0.38465484
## Lag 327680  0.11123941        0.111356563        0.21164986         0.27852000
## Lag 1638400 0.07516871       -0.002982911        0.09513563        -0.06106261
##                 mutual gwesp.OTP.fixed.0.5 gwdsp.OTP.fixed.0.5
## Lag 0       0.79999770          0.88951827          0.87107087
## Lag 32768   0.66026068          0.69041074          0.56750224
## Lag 163840  0.38096094          0.39655308          0.32909183
## Lag 327680  0.07195343          0.12801382          0.08708550
## Lag 1638400 0.11308394          0.09505784          0.04044172
## 
## , , nodematch.eversmk1
## 
##                   edges nodematch.hispanic nodematch.female1 nodematch.eversmk1
## Lag 0        0.84731435          0.7724498        0.79308088          1.0000000
## Lag 32768    0.54365021          0.5122084        0.63731624          0.6624233
## Lag 163840   0.31661036          0.3735145        0.38613833          0.4631210
## Lag 327680   0.12487907          0.1838576        0.21306300          0.2895293
## Lag 1638400 -0.04843904         -0.0871528       -0.05860075         -0.1732522
##                  mutual gwesp.OTP.fixed.0.5 gwdsp.OTP.fixed.0.5
## Lag 0        0.73949417          0.82596806          0.82962588
## Lag 32768    0.59917271          0.64206417          0.53636921
## Lag 163840   0.36156912          0.38961111          0.32502461
## Lag 327680   0.06513275          0.10756201          0.12157020
## Lag 1638400 -0.02126220         -0.05784788         -0.05300152
## 
## , , mutual
## 
##                   edges nodematch.hispanic nodematch.female1 nodematch.eversmk1
## Lag 0       0.832969818          0.6902554        0.79999770         0.73949417
## Lag 32768   0.655957685          0.5420351        0.68082349         0.60650896
## Lag 163840  0.453711697          0.3807566        0.46832909         0.47654529
## Lag 327680  0.189592365          0.1950812        0.25444882         0.34592646
## Lag 1638400 0.004326463         -0.0397559        0.03453263        -0.04956656
##                 mutual gwesp.OTP.fixed.0.5 gwdsp.OTP.fixed.0.5
## Lag 0       1.00000000          0.91166903         0.790126039
## Lag 32768   0.77089766          0.75016262         0.613992396
## Lag 163840  0.51073753          0.53492576         0.445401161
## Lag 327680  0.19116258          0.22568907         0.144338541
## Lag 1638400 0.01557354          0.02072621        -0.002615637
## 
## , , gwesp.OTP.fixed.0.5
## 
##                  edges nodematch.hispanic nodematch.female1 nodematch.eversmk1
## Lag 0       0.91366631         0.79556426        0.88951827         0.82596806
## Lag 32768   0.65221015         0.57748172        0.71103822         0.63534710
## Lag 163840  0.40355191         0.36375124        0.42906065         0.45848417
## Lag 327680  0.16182896         0.15751100        0.23871746         0.30543634
## Lag 1638400 0.02774368        -0.01550744        0.04360474        -0.05912761
##                 mutual gwesp.OTP.fixed.0.5 gwdsp.OTP.fixed.0.5
## Lag 0       0.91166903          1.00000000          0.88286005
## Lag 32768   0.75714027          0.74743488          0.62020864
## Lag 163840  0.47254922          0.48618158          0.40054594
## Lag 327680  0.14530942          0.18887509          0.12356707
## Lag 1638400 0.05355936          0.04005611          0.01544559
## 
## , , gwdsp.OTP.fixed.0.5
## 
##                  edges nodematch.hispanic nodematch.female1 nodematch.eversmk1
## Lag 0       0.97089215         0.82655175        0.87107087         0.82962588
## Lag 32768   0.56904543         0.49933571        0.63747170         0.51566990
## Lag 163840  0.31817376         0.32249022        0.37414872         0.32999678
## Lag 327680  0.15987338         0.11941690        0.21123819         0.24152798
## Lag 1638400 0.01040193        -0.02676337        0.01558998        -0.05445063
##                 mutual gwesp.OTP.fixed.0.5 gwdsp.OTP.fixed.0.5
## Lag 0       0.79012604           0.8828601          1.00000000
## Lag 32768   0.64720629           0.6437981          0.56197239
## Lag 163840  0.40245842           0.4041699          0.32130564
## Lag 327680  0.09213271           0.1437246          0.12697167
## Lag 1638400 0.06161009           0.0289774         -0.01011366
  1. Diagnóstico de Geweke: Del archivo de ayuda de la función:

“Si las muestras se extraen de la distribución estacionaria de la cadena, las dos medias son iguales y la estadística de Geweke tiene una distribución normal estándar asintóticamente. […] El Z-score se calcula bajo la suposición de que las dos partes de la cadena son asintóticamente independientes, lo que requiere que la suma de frac1 y frac2 sea estrictamente menor que 1.”

—?coda::geweke.diag

Echemos un vistazo a una sola cadena:

coda::geweke.diag(sample_uncentered)[[1]]
## 
## Fraction in 1st window = 0.1
## Fraction in 2nd window = 0.5 
## 
##               edges  nodematch.hispanic   nodematch.female1  nodematch.eversmk1 
##             -1.0828             -0.9888             -1.7401             -0.8217 
##              mutual gwesp.OTP.fixed.0.5 gwdsp.OTP.fixed.0.5 
##             -1.4265             -1.1219             -0.8655
  1. (no incluido) Diagnóstico de Gelman: Del archivo de ayuda de la función:

Gelman y Rubin (1992) proponen un enfoque general para monitorear la convergencia de salida MCMC en el que se ejecutan m > 1 cadenas paralelas con valores iniciales que están sobre-dispersos relativo a la distribución posterior. La convergencia se diagnostica cuando las cadenas han ‘olvidado’ sus valores iniciales, y la salida de todas las cadenas es indistinguible. El diagnóstico gelman.diag se aplica a una sola variable de la cadena. Se basa en una comparación de varianzas dentro de cadena y entre cadenas, y es similar a un análisis de varianza clásico. —?coda::gelman.diag

Como diferencia del estadístico de diagnóstico anterior, este usa todas las cadenas simultáneamente:

coda::gelman.diag(sample_uncentered)
## Potential scale reduction factors:
## 
##                     Point est. Upper C.I.
## edges                     1.05       1.14
## nodematch.hispanic        1.02       1.04
## nodematch.female1         1.07       1.20
## nodematch.eversmk1        1.07       1.22
## mutual                    1.07       1.20
## gwesp.OTP.fixed.0.5       1.09       1.26
## gwdsp.OTP.fixed.0.5       1.06       1.18
## 
## Multivariate psrf
## 
## 1.15

Como regla general, valores en el [.9,1.1] son buenos.

Una característica agradable de la función mcmc.diagnostics son los gráficos bonitos de traza y distribución posterior que genera. Si tienes el paquete de R latticeExtra (Sarkar and Andrews 2022), la función anulará los gráficos predeterminados usados por coda::plot.mcmc y usará lattice en su lugar, creando gráficos de mejor apariencia. El siguiente fragmento de código llama la función mcmc.diagnostic, pero suprimimos el resto de la salida (ver figura ?fig-coda-plots).

# [2022-03-13] Esta línea está fallando por lo que podría ser un error de ergm
# mcmc.diagnostics(ans0, center = FALSE) # Suprimiendo toda la salida

Si llamamos la función mcmc.diagnostics, este mensaje aparece al final:

Los diagnósticos MCMC mostrados aquí son de la última ronda de simulación, previo al cálculo de las estimaciones finales de parámetros. Porque las estimaciones finales son refinamientos de aquellas usadas para esta ejecución de simulación, estos diagnósticos pueden subestimar el rendimiento del modelo. Para evaluar directamente el rendimiento del modelo final en estadísticas del modelo, por favor usa el comando GOF: gof(ergmFitObject, GOF=~model).

—mcmc.diagnostics(ans0)

¡No está tan mal (aunque el término mutual podría hacerlo mejor)!3 Primero, observa que en la figura, vemos cuatro líneas diferentes; ¿por qué es eso? Dado que estábamos ejecutando en paralelo usando cuatro núcleos, el algoritmo ejecutó cuatro cadenas del algoritmo MCMC. Una prueba visual es ver si todas las cadenas se movieron más o menos al mismo lugar; en tal caso, podemos empezar a pensar sobre convergencia del modelo desde la perspectiva MCMC.

Una vez que estamos seguros de haber alcanzado convergencia en el algoritmo MCMC, podemos empezar a pensar sobre qué tan bien nuestro modelo predice las propiedades de la red observada. Además de las estadísticas que definen nuestro ERGM, el comportamiento predeterminado de la función gof muestra GOF para:

  1. Distribución de grado de entrada,
  2. Distribución de grado de salida,
  3. Socios compartidos por enlace, y
  4. Geodésicas

Echemos un vistazo

# Calculando e imprimiendo estadísticas GOF
ans_gof <- gof(ans2)
ans_gof
## 
## Goodness-of-fit for in-degree 
## 
##           obs min  mean max MC p-value
## idegree0   13   1  6.36  12       0.00
## idegree1   34  12 20.37  30       0.00
## idegree2   37  21 34.82  51       0.80
## idegree3   48  30 46.34  66       0.82
## idegree4   37  38 52.81  67       0.00
## idegree5   47  42 54.17  72       0.36
## idegree6   42  34 48.49  66       0.44
## idegree7   39  21 41.75  59       0.70
## idegree8   35  15 34.14  51       0.86
## idegree9   21  14 25.98  38       0.44
## idegree10  12   9 19.11  35       0.12
## idegree11  19   4 13.15  21       0.14
## idegree12   4   3  8.53  16       0.12
## idegree13   7   1  5.25  11       0.58
## idegree14   6   0  3.31   8       0.18
## idegree15   3   0  1.67   6       0.48
## idegree16   4   0  0.82   6       0.06
## idegree17   3   0  0.53   4       0.04
## idegree18   3   0  0.26   2       0.00
## idegree19   2   0  0.10   2       0.02
## idegree20   1   0  0.04   2       0.06
## idegree22   1   0  0.00   0       0.00
## 
## Goodness-of-fit for out-degree 
## 
##           obs min  mean max MC p-value
## odegree0    4   2  6.90  14       0.26
## odegree1   28  10 19.15  30       0.06
## odegree2   45  23 32.45  46       0.02
## odegree3   50  27 44.37  60       0.40
## odegree4   54  34 52.97  71       0.96
## odegree5   62  38 53.24  72       0.18
## odegree6   40  39 51.80  75       0.02
## odegree7   28  32 45.95  61       0.00
## odegree8   13  22 34.51  52       0.00
## odegree9   16  17 27.64  39       0.00
## odegree10  20  11 19.13  28       0.92
## odegree11   8   2 12.76  20       0.18
## odegree12  11   2  8.08  14       0.42
## odegree13  13   0  4.18  10       0.00
## odegree14   6   0  2.49   7       0.06
## odegree15   6   0  1.15   4       0.00
## odegree16   7   0  0.68   4       0.00
## odegree17   4   0  0.22   3       0.00
## odegree18   3   0  0.15   1       0.00
## odegree19   0   0  0.06   1       1.00
## odegree20   0   0  0.10   2       1.00
## odegree22   0   0  0.01   1       1.00
## odegree23   0   0  0.01   1       1.00
## 
## Goodness-of-fit for edgewise shared partner 
## 
##           obs min    mean  max MC p-value
## esp.OTP0 1032 991 1046.85 1114       0.60
## esp.OTP1  755 777  830.99  905       0.00
## esp.OTP2  352 288  355.30  414       0.78
## esp.OTP3  202 101  122.85  148       0.00
## esp.OTP4   79  25   39.83   54       0.00
## esp.OTP5   36   3    9.82   26       0.00
## esp.OTP6   14   0    2.26    9       0.00
## esp.OTP7    4   0    0.53    2       0.00
## esp.OTP8    1   0    0.08    1       0.16
## 
## Goodness-of-fit for minimum geodesic distance 
## 
##       obs   min     mean   max MC p-value
## 1    2475  2308  2408.51  2618       0.10
## 2   10672  9717 10526.74 12093       0.62
## 3   31134 32726 36472.28 42060       0.00
## 4   50673 62083 66619.95 71128       0.00
## 5   42563 36051 41272.32 45938       0.44
## 6   18719  6165  9506.31 14061       0.00
## 7    4808   481  1321.87  2588       0.00
## 8     822    11   143.17   505       0.00
## 9     100     0    12.69   269       0.02
## 10      7     0     1.21    84       0.02
## 11      0     0     0.13    12       1.00
## Inf 12333  2904  6020.82 11478       0.00
## 
## Goodness-of-fit for model statistics 
## 
##                           obs       min      mean       max MC p-value
## edges                2475.000  2308.000  2408.510  2618.000       0.10
## nodematch.hispanic   1832.000  1667.000  1758.880  1860.000       0.08
## nodematch.female1    1879.000  1696.000  1771.860  1957.000       0.04
## nodematch.eversmk1   1755.000  1604.000  1702.570  1880.000       0.24
## mutual                486.000   428.000   448.360   465.000       0.00
## gwesp.OTP.fixed.0.5  1775.406  1506.382  1601.146  1792.351       0.02
## gwdsp.OTP.fixed.0.5 13187.633 11655.503 12574.732 14495.043       0.12

# Graficando estadísticas GOF
plot(ans_gof)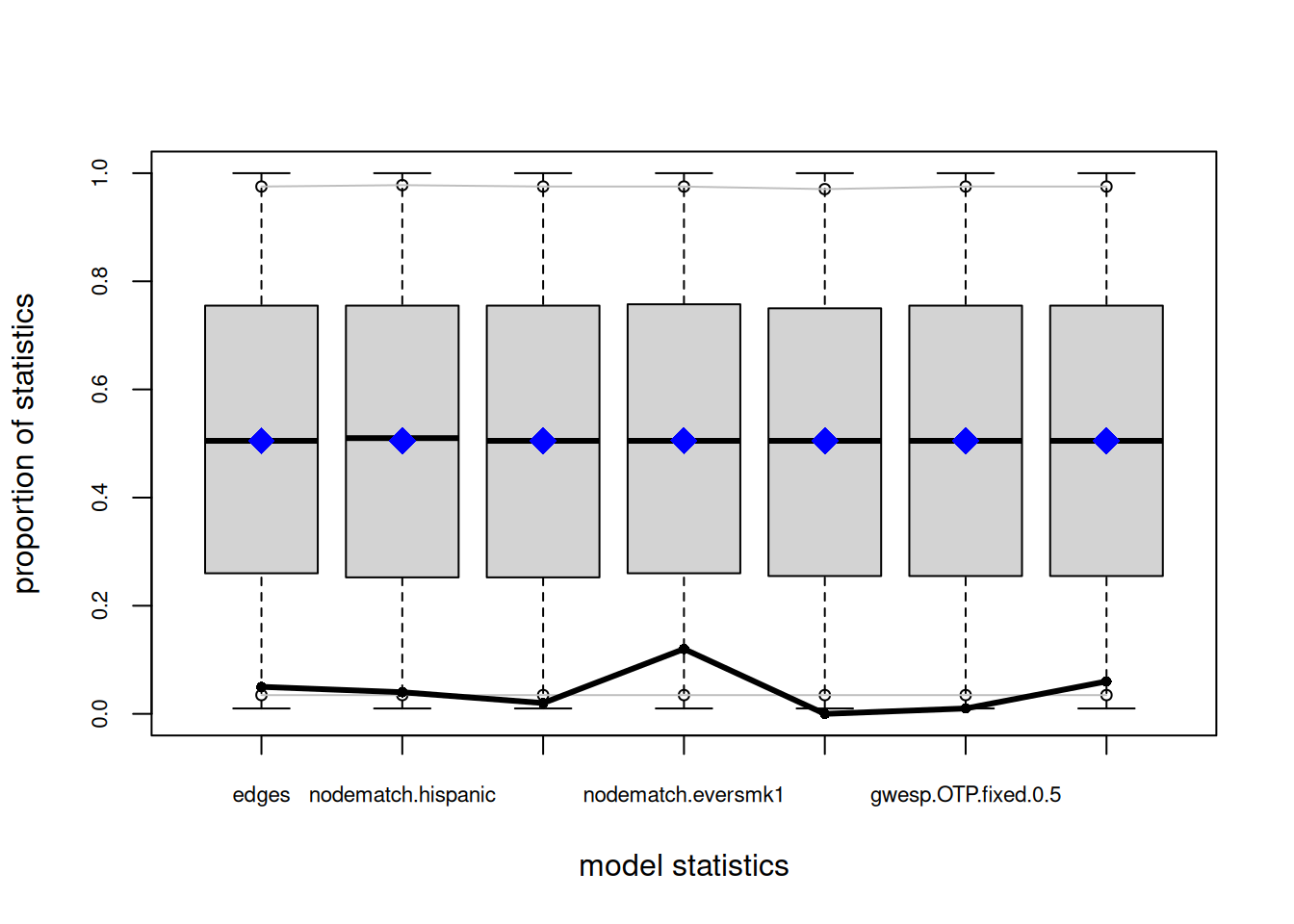

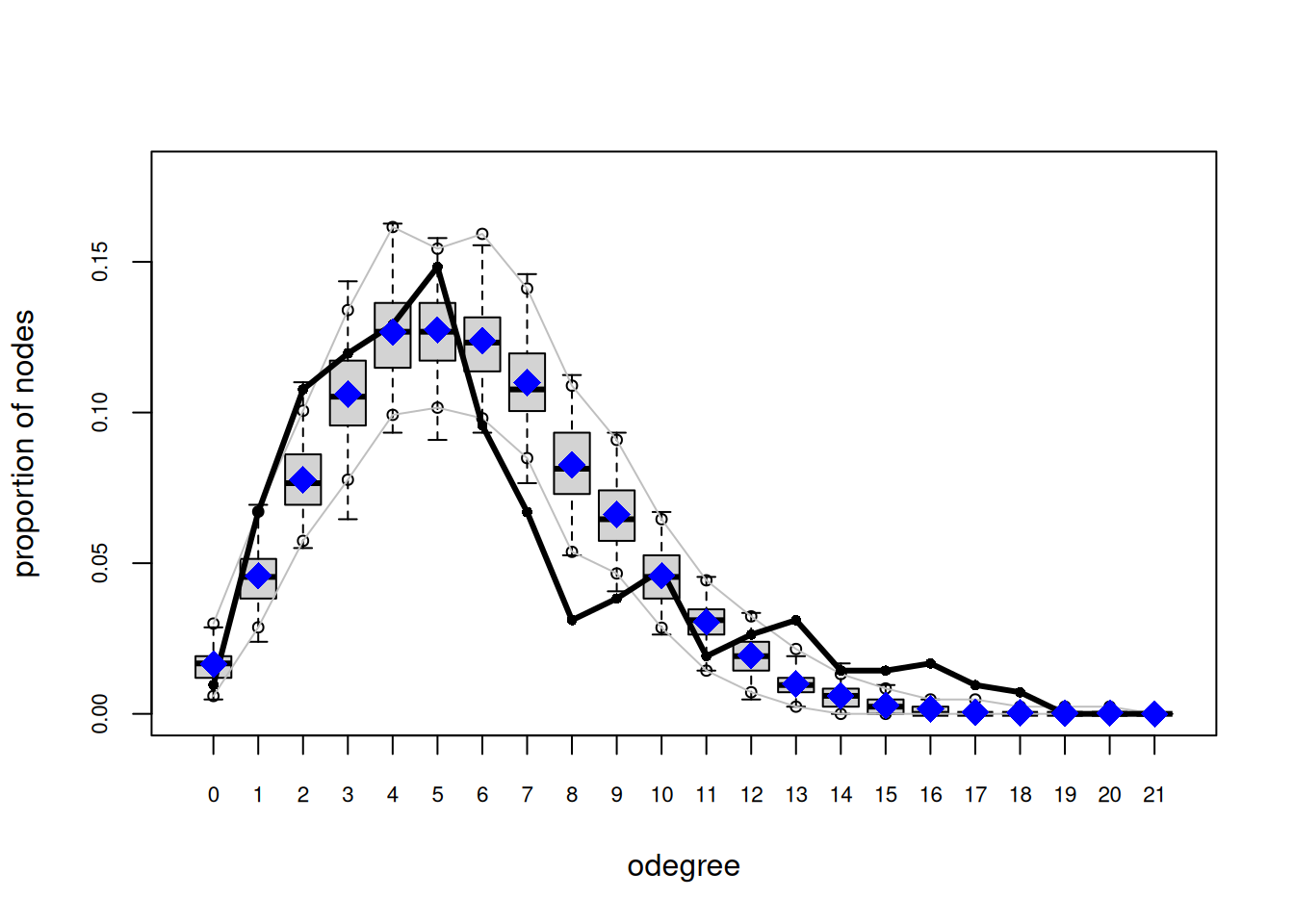
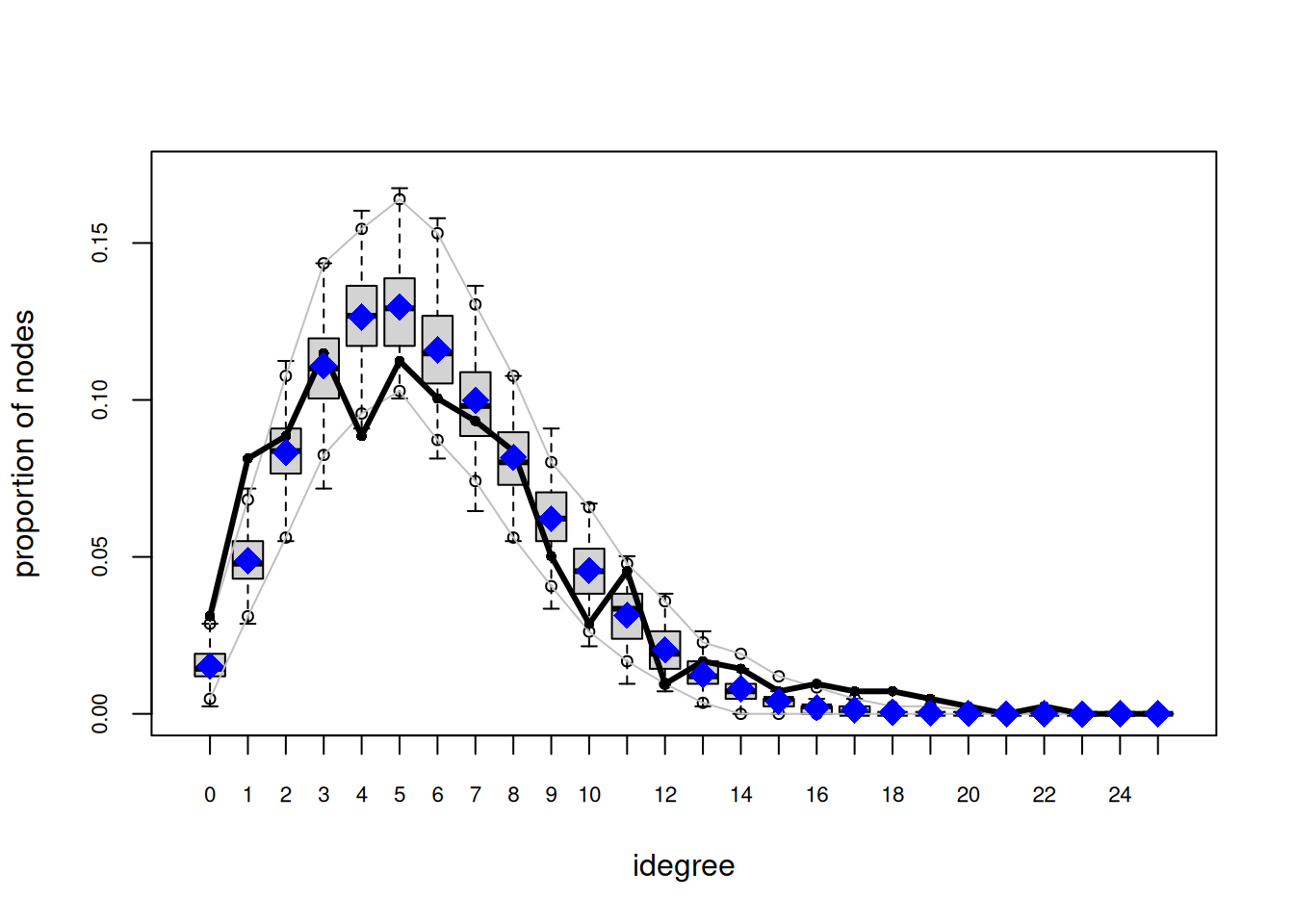
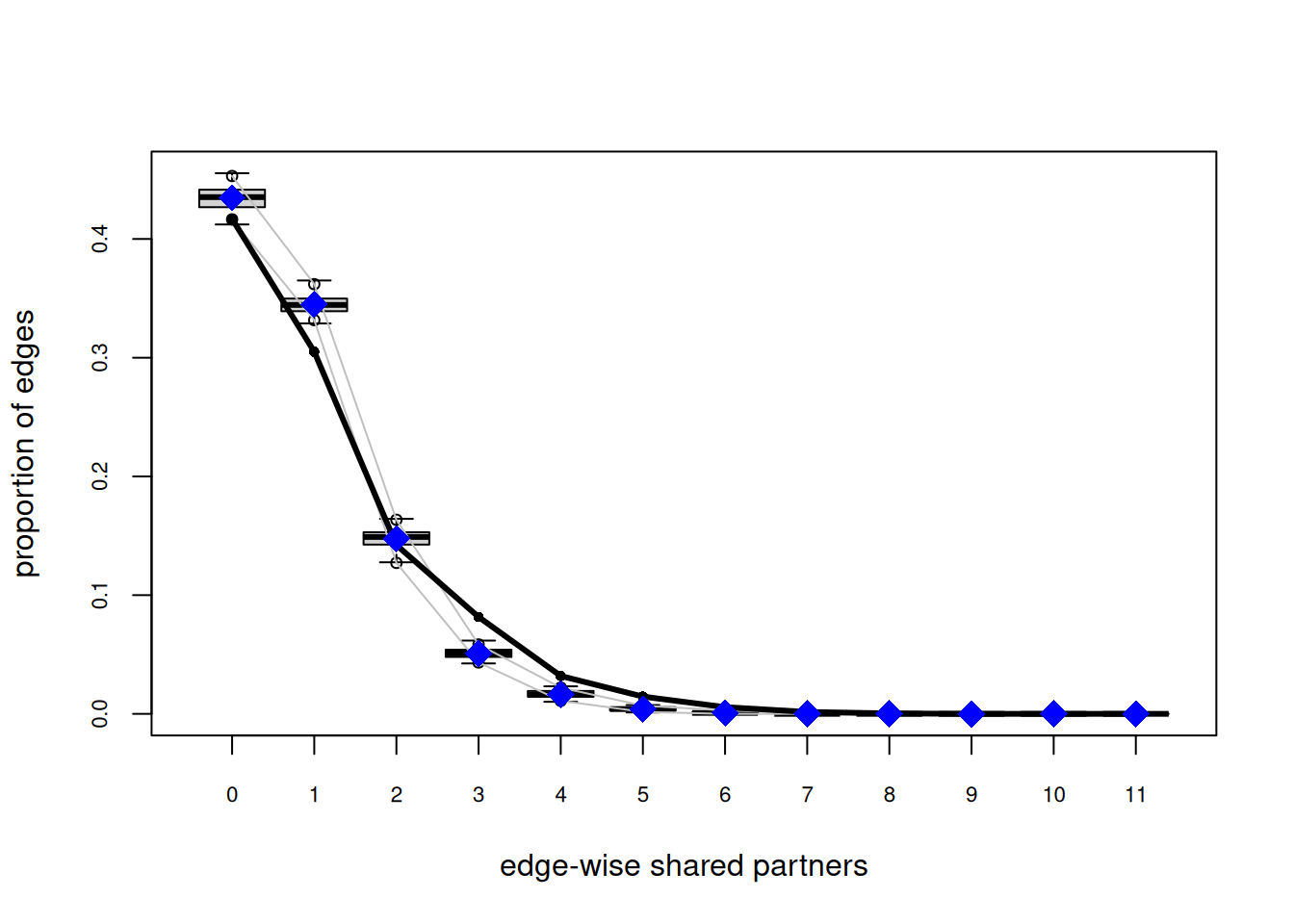
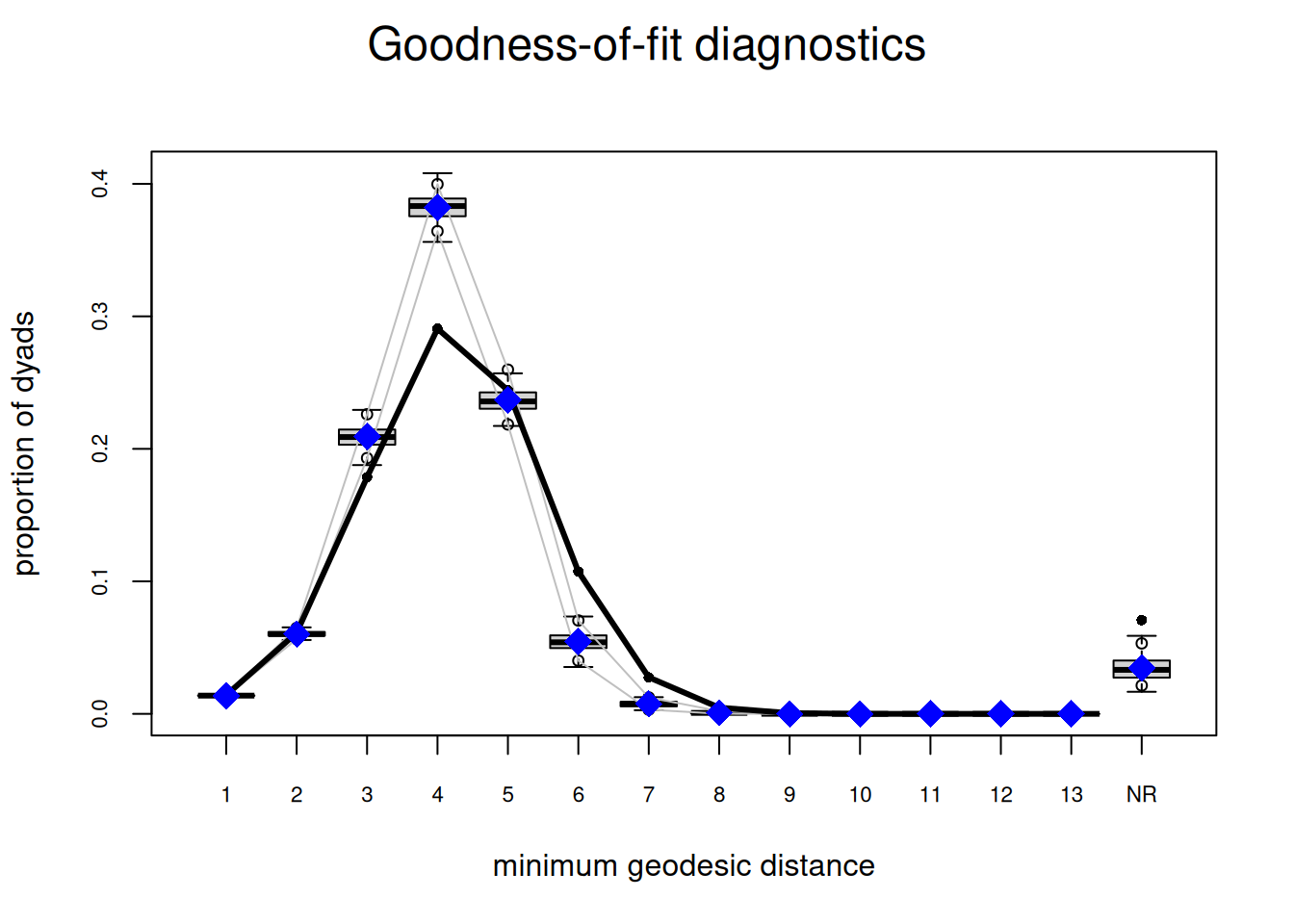
Prueba la siguiente configuración en su lugar

ans0_bis <- ergm(
  network_111 ~
    edges +
    nodematch("hispanic") +
    nodematch("female1") +
    mutual + 
    esp(0:3) + 
    idegree(0:10)
    ,
  constraints = ~bd(maxout = 19),
  control = control.ergm(
    seed        = 1,
    MCMLE.maxit = 15,
    parallel    = 4,
    CD.maxit    = 15,
    MCMC.samplesize = 2048*4,
    MCMC.burnin = 30000,
    MCMC.interval = 2048*4
    )
  )

Aumentar el tamaño de muestra, para que las curvas sean más suaves, intervalos más largos (adelgazamiento), lo que reduce la autocorrelación, y un quemado más grande. Todo esto junto para mejorar la estadística de prueba de Gelman. También agregamos idegree del 0 al 10, y esp del 0 al 3 para coincidir explícitamente con esas estadísticas en nuestro modelo.

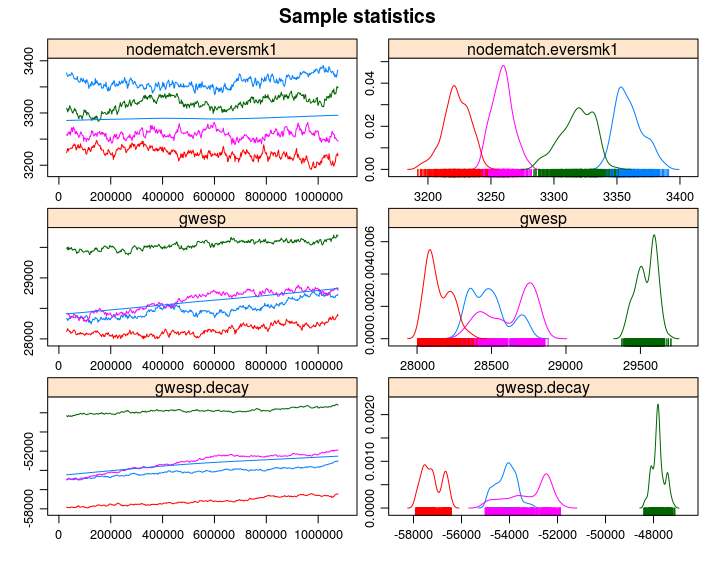
Un ejemplo de un ERGM terrible (no hay convergencia en absoluto). También, un buen ejemplo de por qué ejecutar múltiples cadenas puede ser útil

Más sobre convergencia MCMC

Para más sobre este tema, recomiendo revisar capítulo 1 y capítulo 6 del Manual de MCMC (Brooks et al. 2011). Ambos capítulos están disponibles para descarga gratuita desde el sitio web del libro.

Para GOF echa un vistazo a la sección 6 del tutorial ERGM 2016 Sunbelt, y para una revisión más técnica, puedes echar un vistazo a (David R. Hunter, Goodreau, and Handcock 2008).

Interpretación Matemática

Una de las partes más críticas del modelado estadístico es interpretar los resultados, si no la más importante. En el caso de ERGMs, un aspecto clave se basa en estadísticas de cambio. Supón que nos gustaría saber qué tan probable es que el vínculo y_{ij} ocurra, dada el resto de la red. Podemos calcular tales probabilidades usando lo que la literatura a veces describe como el muestreador de Gibbs.

En particular, las log-odds del vínculo ij ocurriendo condicional en el resto de la red pueden escribirse como:

\begin{equation} \text{logit}\left({\Pr{y_{ij} = 1|y_{-ij}}}\right) = {\theta}^\mathbf{t}\Delta\delta\left(y_{ij}:0\to 1\right), \end{equation}

con \delta\left(y_{ij}:0\to 1\right)\equiv s\left(\mathbf{y}\right)_{\text{ij}}^+ - s\left(\mathbf{y}\right)_{\text{ij}}^- como el vector de estadísticas de cambio, en otras palabras, la diferencia entre las estadísticas suficientes cuando y_{ij}=1 y su valor cuando y_{ij} = 0. Para mostrar esto, escribimos lo siguiente:

\begin{align*} \Pr{y_{ij} = 1|y_{-ij}} & = % \frac{\Pr{y_{ij} = 1, x_{-ij}}}{% {\mathbb{P}_{+}\left(y_{ij} = 1, y_{-ij}\right) } \Pr{y_{ij} = 0, y_{-ij}}} \\ & = \frac{\text{exp}\left\{{\theta}^\mathbf{t}s\left(\mathbf{y}\right)^+_{ij}\right\}}{% \text{exp}\left\{{\theta}^\mathbf{t}s\left(\mathbf{y}\right)^+_{ij}\right\} + \text{exp}\left\{{\theta}^\mathbf{t}s\left(\mathbf{y}\right)^-_{ij}\right\}} \end{align*}

Aplicando la función logit a la ecuación anterior, obtenemos:

\begin{align*} & = \text{log}\left\{\frac{\text{exp}\left\{{\theta}^\mathbf{t}s\left(\mathbf{y}\right)^+_{ij}\right\}}{% \text{exp}\left\{{\theta}^\mathbf{t}s\left(\mathbf{y}\right)^+_{ij}\right\} + % \text{exp}\left\{{\theta}^\mathbf{t}s\left(\mathbf{y}\right)^-_{ij}\right\}}\right\} - % \text{log}\left\{ % \frac{\text{exp}\left\{{\theta}^\mathbf{t}s\left(\mathbf{y}\right)^-_{ij}\right\}}{% \text{exp}\left\{{\theta}^\mathbf{t}s\left(\mathbf{y}\right)^+_{ij}\right\} + \text{exp}\left\{{\theta}^\mathbf{t}s\left(\mathbf{y}\right)^-_{ij}\right\}}% \right\} \\ & = \text{log}\left\{\text{exp}\left\{{\theta}^\mathbf{t}s\left(\mathbf{y}\right)^+_{ij}\right\}\right\} - \text{log}\left\{\text{exp}\left\{{\theta}^\mathbf{t}s\left(\mathbf{y}\right)^-_{ij}\right\}\right\} \\ & = {\theta}^\mathbf{t}\left(s\left(\mathbf{y}\right)^+_{ij} - s\left(\mathbf{y}\right)^-_{ij}\right) \\ & = {\theta}^\mathbf{t}\Delta\delta\left(y_{ij}:0\to 1\right) \end{align*} Por lo tanto, la probabilidad condicional del nodo n ganando función k puede escribirse como:

\begin{equation} {\mathbb{P}_{=}\left(y_{ij} = 1|y_{-ij}\right) } \frac{1}{1 + \text{exp}\left\{-{\theta}^\mathbf{t}\Delta\delta\left(y_{ij}:0\to 1\right)\right\}} \end{equation}

es decir, una probabilidad logística.

Independencia de Markov

El desafío de analizar redes es su naturaleza interdependiente. No obstante, en ausencia de tal interdependencia, los ERGMs son equivalentes a regresión logística. Conceptualmente, si todas las estadísticas incluidas en el modelo no involucran dos o más díadas, entonces el modelo es no-Markoviano en el sentido de grafos de Markov.

Matemáticamente, para ver esto, es suficiente mostrar que la probabilidad ERGM puede escribirse como el producto de las probabilidades de cada díada.

\begin{equation*} {\mathbb{P}_{=}\left(\mathbf{y} | \theta\right) } \frac{\text{exp}\left\{{\theta}^\mathbf{t}s\left(\mathbf{y}\right)\right\}}{\sum_{y}\text{exp}\left\{{\theta}^\mathbf{t}s\left(\mathbf{y}\right)\right\}} = \frac{\prod_{ij}\text{exp}\left\{{\theta}^\mathbf{t}s\left(\mathbf{y}\right)_{ij}\right\}}{\sum_{y}\text{exp}\left\{{\theta}^\mathbf{t}s\left(\mathbf{y}\right)\right\}} \end{equation*}

Donde s\left(\right)_{ij} es una función tal que s\left(\mathbf{y}\right) = \sum_{ij}{s\left(\mathbf{y}\right)_{ij}}. Ahora necesitamos tratar con la constante normalizadora. Para ver cómo eso puede separarse, comencemos desde el resultado:

\begin{align*} & =\prod_{ij}\left(1 + \text{exp}\left\{{\theta}^\mathbf{t}s\left(\mathbf{y}\right)_{ij}\right\}\right) \\ & = \left(1 + \text{exp}\left\{{\theta}^\mathbf{t}s\left(\mathbf{y}\right)_{11}\right\}\right)\left(1 + \text{exp}\left\{{\theta}^\mathbf{t}s\left(\mathbf{y}\right)_{12}\right\}\right)\dots\left(1 + \text{exp}\left\{{\theta}^\mathbf{t}s\left(\mathbf{y}\right)_{nn}\right\}\right) \\ & = 1 + \text{exp}\left\{{\theta}^\mathbf{t}s\left(\mathbf{y}\right)_{11}\right\} + \text{exp}\left\{{\theta}^\mathbf{t}s\left(\mathbf{y}\right)_{11}\right\}\text{exp}\left\{{\theta}^\mathbf{t}s\left(\mathbf{y}\right)_{12}\right\} + \dots + \prod_{ij}\text{exp}\left\{{\theta}^\mathbf{t}s\left(\mathbf{y}\right)_{ij}\right\} \\ & = 1 + \text{exp}\left\{{\theta}^\mathbf{t}s\left(\mathbf{y}\right)_{11}\right\} + \text{exp}\left\{{\theta}^\mathbf{t}\left(s\left(\mathbf{y}\right)_{11} + s\left(\mathbf{y}\right)_{12}\right)\right\} + \dots + \prod_{ij}\text{exp}\left\{{\theta}^\mathbf{t}s\left(\mathbf{y}\right)_{ij}\right\} \\ & = \sum_{\mathbf{y}\in\mathcal{Y}}\text{exp}\left\{{\theta}^\mathbf{t}s\left(\mathbf{y}\right)\right\} \end{align*}

Donde la última igualdad sigue del hecho de que la suma es la suma sobre todas las combinaciones posibles de redes, comenzando desde exp(0) = 1, hasta exp(all). De esta manera, ahora podemos escribir:

\begin{equation} \frac{\prod_{ij}\text{exp}\left\{{\theta}^\mathbf{t}s\left(\mathbf{y}\right)_{ij}\right\}}{\sum_{y}\text{exp}\left\{{\theta}^\mathbf{t}s\left(\mathbf{y}\right)\right\}} = \prod_{ij}\frac{\text{exp}\left\{{\theta}^\mathbf{t}s\left(\mathbf{y}\right)_{ij}\right\}}{1 + \text{exp}\left\{{\theta}^\mathbf{t}s\left(\mathbf{y}\right)_{ij}\right\}} \end{equation}

Relacionado con esto, los ERGMs bloque-diagonales pueden estimarse como modelos independientes, uno por bloque. Para ver más sobre esto, lee (SNIJDERS 2010). De manera similar, dado que la independencia depende–juego de palabras intencionado–de particionar la función objetivo, como señala Snijders, las funciones no lineales hacen que el modelo sea dependiente, ej., s\left(\mathbf{y}\right) = \sqrt{\sum_{ij}y_{ij}}, la raíz cuadrada del conteo de enlaces ya no es un grafo de Bernoulli.

  1. Puedes descargar el archivo 03.rda desde este enlace.↩︎

  2. Sí, las clases tienen el mismo nombre que los paquetes.↩︎

  3. El sitio web wiki de statnet tiene un ejemplo muy agradable de gráficos de diagnóstico MCMC (muy) malos y buenos aquí.↩︎