# Diseño
n_sims <- 500 # Número de simulaciones
n_a <- 4 # Número de alters
sizes <- # Tamaños a probar
seq(from = 100, to = 200, by = 25)
# Suposiciones
odds_h_1 <- 2.0 # Odds de Aumento/
attrition <- .3
baseline <- .2 # Baja prevalencia en 1s
# Parámetros
alpha <- .05
beta_pow <- 0.2Cálculo de poder en estudios de redes
Esta versión del capítulo fue traducida de manera automática utilizando IA. El capítulo aún no ha sido revisado por un humano.
En el diseño de encuestas y estudios, calcular el tamaño de muestra requerido es crítico. Hoy en día, abundan las herramientas y métodos para calcular el tamaño de muestra requerido; no obstante, el cálculo de tamaño de muestra para estudios que involucran redes sociales aún está subdesarrollado. Este capítulo ilustrará cómo podemos usar simulaciones por computadora para estimar el tamaño de muestra requerido. El Capítulo Poder y tamaño de muestra proporciona una vista general del análisis de poder.
Ejemplo 1: Efectos de derrame en estudios egocéntricos1
Supón que queremos ejecutar una intervención sobre una población particular, y estamos interesados en los efectos de tal intervención en los alters de los egos. En economía, este problema, que llaman el “efecto de derrame,” se estudia activamente.
Asumimos que los alters solo se exponen si los egos adquieren el comportamiento para el cálculo de poder. Además, para esta primera ejecución, asumiremos que no hay refuerzo social o influencia entre alters. Posteriormente relajaremos esta suposición. Para calcular el poder, haremos lo siguiente:
Simular el comportamiento de los egos siguiendo una distribución logit.
Eliminar aleatoriamente algunos egos como resultado de la deserción.
Simular el comportamiento de los alters usando sus egos como el tratamiento.
Ajustar una regresión logística basada en el modelo anterior.
Aceptar/rechazar la nula y almacenar el resultado.
Los pasos anteriores se repetirán 500 veces para cada valor de n que analicemos. Finalizaremos graficando el poder contra los tamaños de muestra. Comencemos primero escribiendo los parámetros de simulación:
Como discutimos en Poder y tamaño de muestra, siempre es una buena idea encapsular la simulación en una función:
# Los odds convertidos a una prob
theta_h_1 <- plogis(log(odds_h_1))
# Función de simulación
sim_data <- function(n) {
# Asignación de tratamiento
tr <- c(rep(1, n/2), rep(0, n/2))
# Paso 1: Muestreando población de egos
y_ego <- runif(n) < c(
rep(theta_h_1, n/2),
rep(0.5, n/2)
)
# Paso 2: Simulando deserción
todrop <- order(runif(n))[1:(n * attrition)]
y_ego <- y_ego[-todrop]
tr <- tr[-todrop]
n <- n - length(todrop)
# Paso 3: Simulando efecto del alter. Asumimos lo mismo que en
# ego
tr_alter <- rep(y_ego * tr, n_a)
y_alter <- runif(n * n_a) < ifelse(tr_alter, theta_h_1, 0.5)
# Paso 4: Calculando estadística de prueba
res_ego <- tryCatch(glm(y_ego ~ tr, family = binomial("logit")), error = function(e) e)
res_alter <- tryCatch(glm(y_alter ~ tr_alter, family = binomial("logit")), error = function(e) e)
if (inherits(res_ego, "error") | inherits(res_alter, "error"))
return(c(ego = NA, alter = NA))
# Paso 5: ¿Rechazar?
c(
ego = summary(res_ego)$coefficients["tr", "Pr(>|z|)"] < alpha,
alter = summary(res_alter)$coefficients["tr_alter", "Pr(>|z|)"] < alpha
)
}Ahora que tenemos la función de generación de datos, podemos ejecutar las simulaciones para aproximar el poder estadístico dado el tamaño de muestra. Los resultados se almacenarán en la matriz spower. Dado que estamos simulando datos, es crucial establecer la semilla para que podamos reproducir los resultados.
# Siempre establecemos la semilla
set.seed(88)
# Haciendo espacio, ¡y ejecutando!
spower <- NULL
for (s in sizes) {
# Ejecutar la simulación para el tamaño s
simres <- rowMeans(replicate(n_sims, sim_data(s)), na.rm = TRUE)
# Y almacenar los resultados
spower <- rbind(spower, simres)
}La siguiente figura muestra el poder aproximado para encontrar efectos en ambos niveles, ego y alter:
library(ggplot2)
spower <- rbind(
data.frame(size = sizes, power = spower[,"ego"], type = "ego"),
data.frame(size = sizes, power = spower[,"alter"], type = "alter")
)
spower |>
ggplot(aes(x = size, y = power, colour = type)) +
geom_point() +
geom_smooth(method = "loess", formula = y ~ x) +
labs(x = "Número de Egos", y = "Poder Aprox.", colour = "Tipo de nodo") +
geom_hline(yintercept = 1 - beta_pow)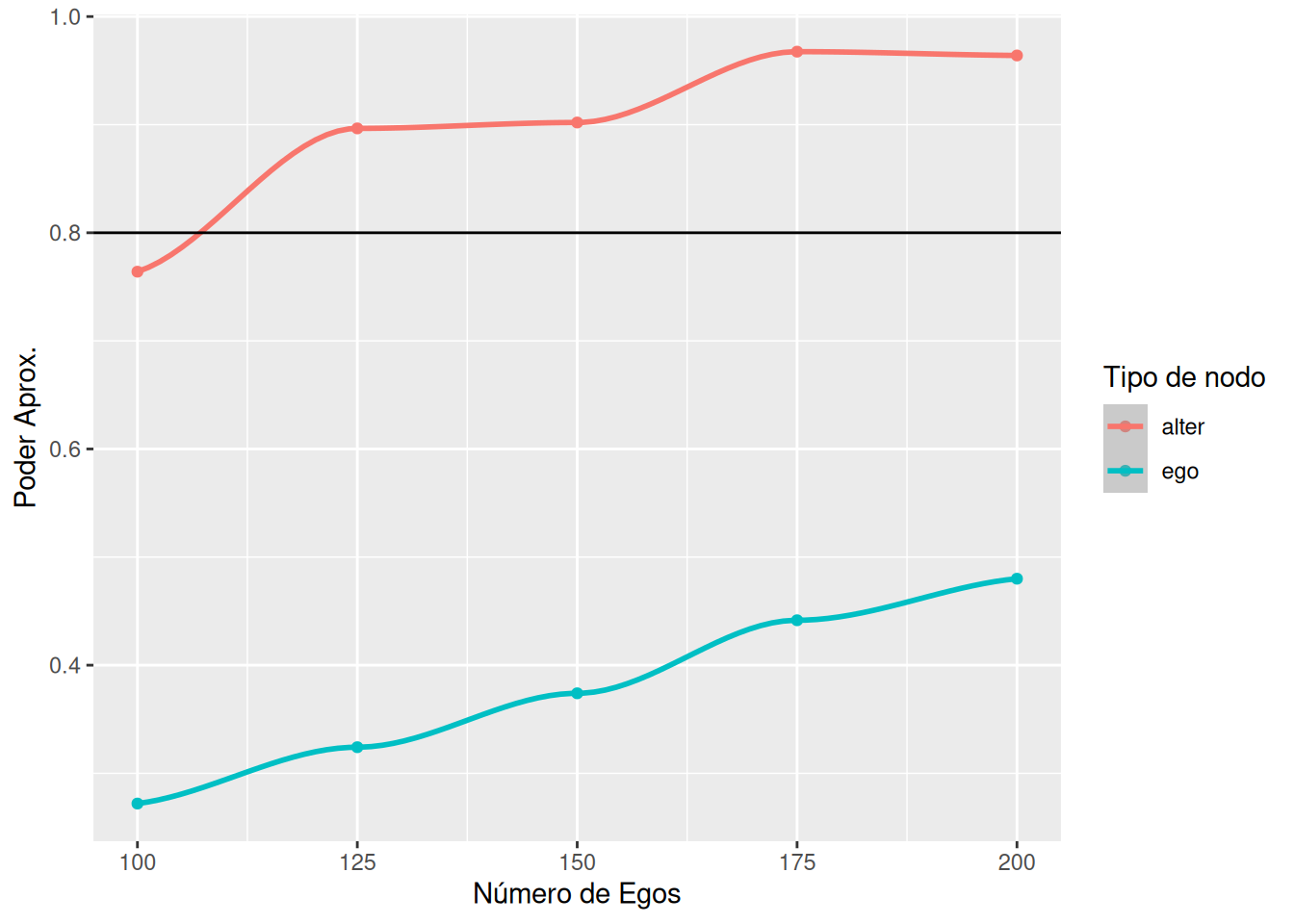
Como se muestra en el Capítulo Poder y tamaño de muestra, podemos usar un modelo de regresión lineal para predecir el tamaño de muestra como una función del poder estadístico:
# Ajustando el modelo
power_model <- glm(
size ~ power + I(power^2),
data = spower, family = gaussian(), subset = type == "alter"
)
summary(power_model)
Call:
glm(formula = size ~ power + I(power^2), family = gaussian(),
data = spower, subset = type == "alter")
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 1460 1342 1.088 0.390
power -3532 3124 -1.131 0.376
I(power^2) 2293 1805 1.270 0.332
(Dispersion parameter for gaussian family taken to be 317.0856)
Null deviance: 6250.00 on 4 degrees of freedom
Residual deviance: 634.17 on 2 degrees of freedom
AIC: 46.404
Number of Fisher Scoring iterations: 2# Predecir
predict(power_model, newdata = data.frame(power = .8), type = "response") |>
ceiling() 1
102 De la figura, se hace evidente que, aunque no hay suficiente poder para identificar efectos a nivel ego, porque cada ego trae cinco alters, el tamaño de muestra de alter es lo suficientemente alto como para que podamos alcanzar por encima de 0.8 de poder estadístico con un tamaño de muestra relativamente pequeño.
Ejemplo 2: Efectos de derrame efecto pre-post
Ahora las dinámicas son diferentes. En lugar de tener un grupo tratado y de control, tenemos un solo grupo sobre el cual mediremos el cambio de comportamiento. Simularemos individuos en su estado inicial, aún 0/1, y luego simularemos que la intervención los hará más propensos a tener y = 1. También asumiremos que los sujetos generalmente no cambian su comportamiento y que la prevalencia basal de ceros es más alta. Los pasos de simulación son los siguientes:
Para cada individuo en la población, extraer la probabilidad subyacente de que y = 1. Con esa probabilidad, asignar el valor de y. Esto aplica tanto para ego como para alter.
Eliminar aleatoriamente algunos egos, y sus alters correspondientes debido a la deserción.
Simular el comportamiento de los alters usando sus egos como el tratamiento. Tanto la probabilidad subyacente de ego como de alter se incrementan por los odds elegidos.
Para controlar la probabilidad subyacente de que un individuo tenga y = 1, usamos regresión logística condicional (también conocida como logit de caso-control pareado,) para estimar los efectos del tratamiento.
Aceptar/rechazar la nula y almacenar el resultado.
beta_pars <- c(4, 6)
odds_h_1 <- 2.0# Función de simulación
library(survival)
sim_data_prepost <- function(n) {
# Paso 1: Muestreando población de egos
y_ego_star <- rbeta(n, beta_pars[1], beta_pars[2])
y_ego_0 <- runif(n) < y_ego_star
# Paso 2: Simulando deserción
todrop <- order(runif(n))[1:(n * attrition)]
y_ego_0 <- y_ego_0[-todrop]
n <- n - length(todrop)
y_ego_star <- y_ego_star[-todrop]
# Paso 3: Simulando efecto del alter. Asumimos lo mismo que en
# ego
y_alter_star <- rbeta(n * n_a, beta_pars[1], beta_pars[2])
y_alter_0 <- runif(n * n_a) < y_alter_star
# Simulando post
y_ego_1 <- runif(n) < plogis(qlogis(y_ego_star) + log(odds_h_1))
tr_alter <- as.integer(rep(y_ego_1, n_a))
y_alter_1 <- runif(n * n_a) < plogis(qlogis(y_alter_star) + log(odds_h_1) * tr_alter) # Así que solo si ego hizo algo
# Paso 4: Calculando estadística de prueba
y_ego_0 <- as.integer(y_ego_0)
y_ego_1 <- as.integer(y_ego_1)
y_alter_0 <- as.integer(y_alter_0)
y_alter_1 <- as.integer(y_alter_1)
d <- data.frame(
y = c(y_ego_0, y_ego_1),
tr = c(rep(0, n), rep(1, n)),
g = c(1:n, 1:n)
)
res_ego <- tryCatch(
clogit(y ~ tr + strata(g), data = d, method = "exact"),
error = function(e) e
)
d <- data.frame(
y = c(y_alter_0, y_alter_1),
tr = c(rep(0, n * n_a), tr_alter),
g = c(1:(n * n_a), 1:(n * n_a))
)
res_alter <- tryCatch(
clogit(y ~ tr + strata(g), data = d, method = "exact"),
error = function(e) e
)
if (inherits(res_ego, "error") | inherits(res_alter, "error"))
return(c(ego = NA, alter = NA))
# Paso 5: ¿Rechazar?
c(
# ego = res_ego$p.value < alpha,
ego = summary(res_ego)$coefficients["tr", "Pr(>|z|)"] < alpha,
alter = summary(res_alter)$coefficients["tr", "Pr(>|z|)"] < alpha,
ego_test = coef(res_ego),
alter_glm = coef(res_alter)
)
}# Siempre establecemos la semilla
set.seed(88)
# ¡Haciendo espacio y ejecutando!
spower <- NULL
for (s in sizes) {
# Ejecutar la simulación para el tamaño s
simres <- rowMeans(
replicate(n_sims, sim_data_prepost(s)),
na.rm = TRUE
)
# Y almacenar los resultados
spower <- rbind(spower, simres)
}library(ggplot2)
spowerd <- rbind(
data.frame(size = sizes, power = spower[,"ego"], type = "ego"),
data.frame(size = sizes, power = spower[,"alter"], type = "alter")
)
spowerd |>
ggplot(aes(x = size, y = power, colour = type)) +
geom_point() +
geom_smooth(method = "loess", formula = y ~ x) +
labs(x = "Número de Egos", y = "Poder Aprox.", colour = "Tipo de nodo") +
geom_hline(yintercept = 1 - beta_pow)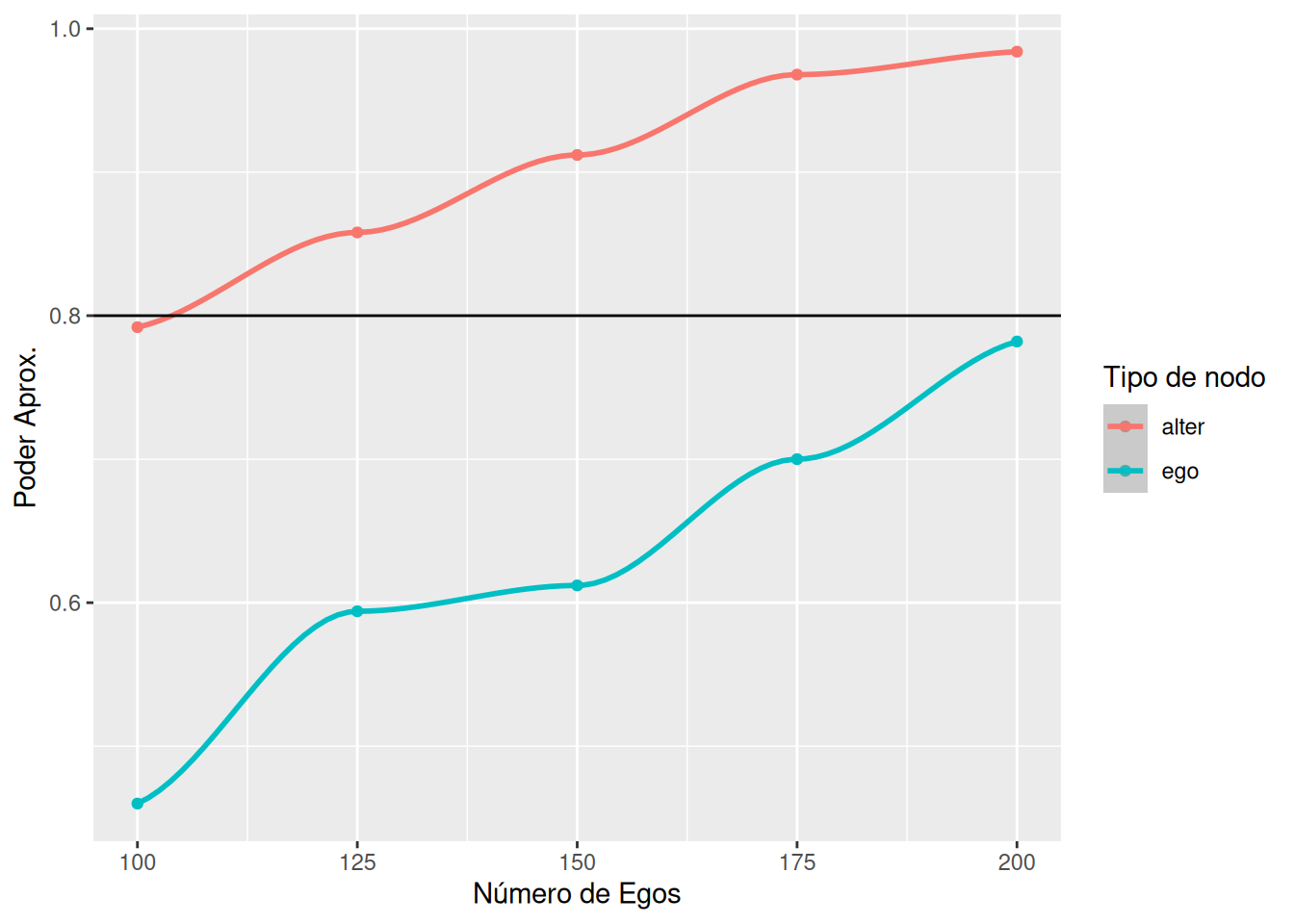
Como se muestra en el Capítulo Poder y tamaño de muestra, podemos usar un modelo de regresión lineal para predecir el tamaño de muestra como una función del poder estadístico:
# Ajustando el modelo
power_model <- glm(
size ~ power + I(power^2),
data = spowerd, family = gaussian(), subset = type == "alter"
)
summary(power_model)
Call:
glm(formula = size ~ power + I(power^2), family = gaussian(),
data = spowerd, subset = type == "alter")
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 611.4 666.3 0.918 0.456
power -1553.8 1504.7 -1.033 0.410
I(power^2) 1147.9 844.8 1.359 0.307
(Dispersion parameter for gaussian family taken to be 52.1536)
Null deviance: 6250.00 on 4 degrees of freedom
Residual deviance: 104.31 on 2 degrees of freedom
AIC: 37.379
Number of Fisher Scoring iterations: 2# Predecir
predict(power_model, newdata = data.frame(power = .8), type = "response") |>
ceiling() 1
104 Ejemplo 3: Primera diferencia
Ahora, en lugar de mirar un resultado dicotómico, evaluemos qué pasa si la variable es continua. Los efectos que estamos interesados en identificar son el efecto ego y alter, \gamma_{ego} y \gamma_{alter}, respectivamente. Además, el proceso de generación de datos es
\begin{align*} y_{itg} & = \alpha_i + \kappa_g + X_i\beta + \varepsilon_{itg} \\ y_{itg} & = \alpha_i + \kappa_g + X_i\beta + D_{i}^{ego}\gamma_{ego} + D_i^{alter}\gamma_{alter} + \varepsilon_{itg} \end{align*}
Donde D_i^{ego/alter} es una variable indicadora. Aquí, el comportamiento de ego y alter están correlacionados a través de un efecto fijo. En otras palabras, dentro de cada grupo, estamos asumiendo que hay una prevalencia basal compartida del resultado. La diferencia principal es que ego y alter pueden tener diferentes resultados con respecto al tamaño del efecto del tratamiento. Otra forma de abordar la correlación a nivel de grupo podría ser a través de un proceso de autocorrelación, como en un modelo autocorrelacionado espacial; no obstante, estimar tales modelos es computacionalmente costoso, así que optamos por usar el anterior.
Para simplicidad, asumimos que no hay efecto de tiempo. Dos componentes esenciales aquí, \alpha_i y \kappa_g son efectos fijos no observados a nivel individual y de grupo. El enfoque más directo aquí es usar un estimador de primera diferencia:
(y_{it+1g} - y_{itg}) = D_{i}^{ego}\gamma_{ego} + D_i^{alter}\gamma_{alter} + \varepsilon'_i, \quad \varepsilon'_i = \varepsilon_{it+1g} - \varepsilon_{itg}
Al tomar la primera diferencia, los efectos fijos se eliminan de la ecuación, y podemos proceder con un modelo lineal regular.
effect_size_ego <- 0.5
effect_size_alter <- 0.25
sizes <- seq(10, 100, by = 10)# Función de simulación
sim_data_prepost <- function(n) {
# Aplicando deserción
n <- floor(n * (1 - attrition))
# Paso 1: Muestreando efectos fijos
alpha_i <- rnorm(n * (n_a + 1))
kappa_g <- rep(rnorm(n_a + 1), n)
# Paso 2: Generando el resultado en t = 1
is_ego <- rep(c(1, rep(0, n_a)), n)
is_alter <- 1 - is_ego
y_0 <- alpha_i + kappa_g + rnorm(n * (n_a + 1))
y_1 <- alpha_i + kappa_g +
is_ego * effect_size_ego +
is_alter * effect_size_alter +
rnorm(n * (n_a + 1))
# Paso 4: Calculando estadística de prueba
res <- tryCatch(
glm(I(y_1 - y_0) ~ -1 + is_ego + is_alter, family = gaussian("identity")),
error = function(e) e
)
if (inherits(res, "error"))
return(c(ego = NA, alter = NA))
# Paso 5: ¿Rechazar?
c(
# ego = res_ego$p.value < alpha,
ego = summary(res)$coefficients["is_ego", "Pr(>|t|)"] < alpha,
alter = summary(res)$coefficients["is_alter", "Pr(>|t|)"] < alpha,
coef(res)[1],
coef(res)[2]
)
}# Siempre establecemos la semilla
set.seed(88)
# ¡Haciendo espacio y ejecutando!
spower <- NULL
for (s in sizes) {
# Ejecutar la simulación para el tamaño s
simres <- rowMeans(
replicate(n_sims, sim_data_prepost(s)),
na.rm = TRUE
)
# Y almacenar los resultados
spower <- rbind(spower, simres)
}library(ggplot2)
spowerd <- rbind(
data.frame(size = sizes, power = spower[,"ego"], type = "ego"),
data.frame(size = sizes, power = spower[,"alter"], type = "alter")
)
spowerd |>
ggplot(aes(x = size, y = power, colour = type)) +
geom_point() +
geom_smooth(method = "loess", formula = y ~ x) +
labs(x = "Número de Egos", y = "Poder Aprox.", colour = "Tipo de nodo") +
geom_hline(yintercept = 1 - beta_pow) +
labs(
caption = sprintf(
"Efecto Ego: %.2f; Efecto Alter: %.2f", effect_size_ego, effect_size_alter)
)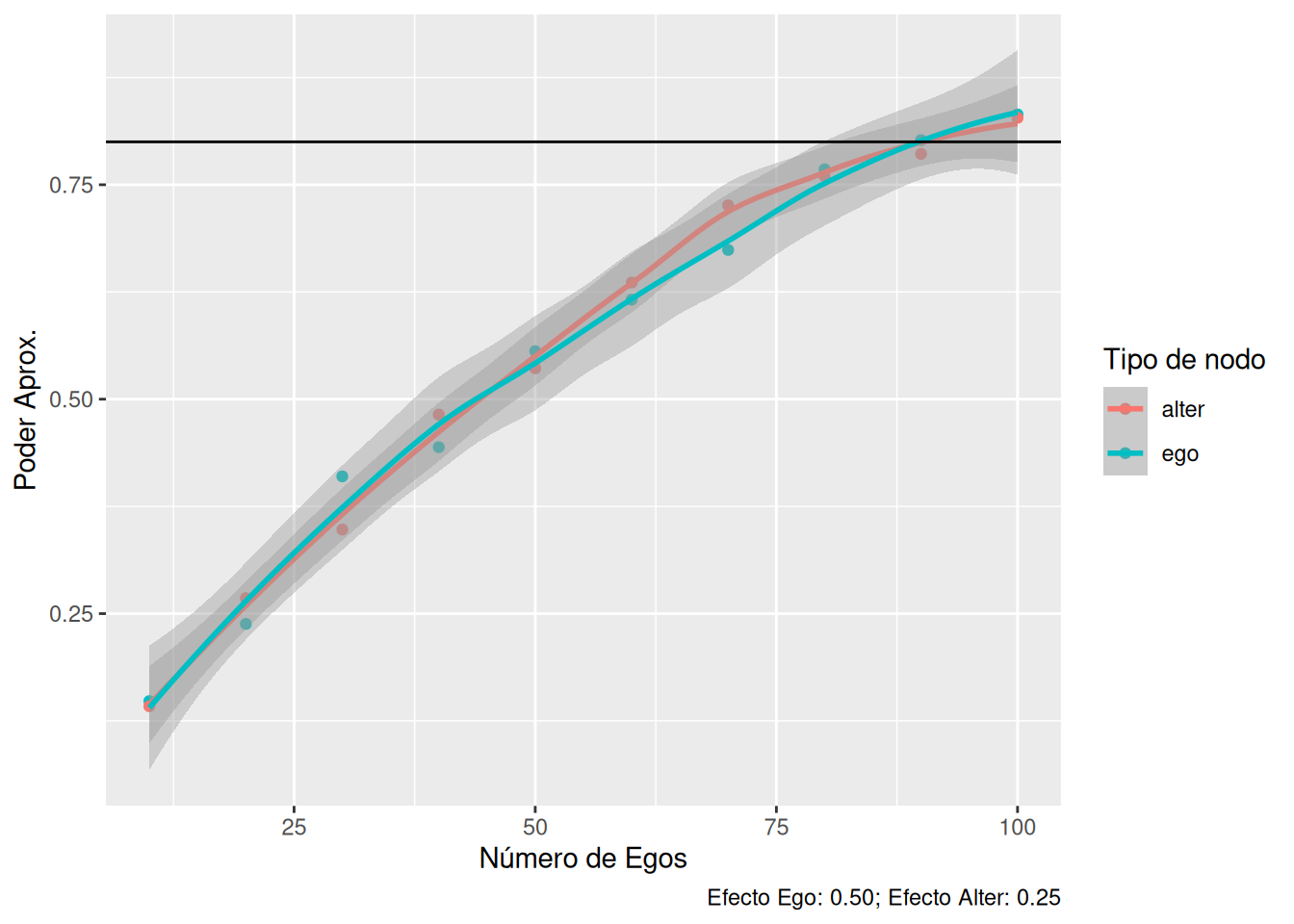
Desde el punto de vista inferencial, aún podríamos usar un operador demean para estimar efectos a nivel individual. En particular, necesitaríamos usar el operador demean a nivel de grupo y luego ajustar un modelo de efecto fijo para estimar parámetros a nivel individual.
El problema original fue planteado por Dr. Shinduk Lee de la Escuela de Enfermería de la Universidad de Utah.↩︎