Simulación y Visualización

Nota de Traducción

Esta versión del capítulo fue traducida de manera automática utilizando IA. El capítulo aún no ha sido revisado por un humano.

En este capítulo, construiremos y visualizaremos redes artificiales utilizando Modelos Exponenciales de Grafos Aleatorios [ERGMs.] Junto con el capítulo 3, este será un ejemplo extendido de cómo leer datos de redes y visualizarlos utilizando algunos de los paquetes de R disponibles.

Para este capítulo, utilizaremos los siguientes paquetes de R:

ergm: Para simular y estimar ERGMs.
sna: Para visualizar redes.
igraph: También para visualizar redes.
intergraph: Para convertir entre objetos igraph y network.
netplot: Nuevamente, para visualización.
netdiffuseR: Para una función única que usamos para ajustar el tamaño de vértices en igraph.
rgexf: Para construir figuras interactivas (html).

Puedes usar el siguiente bloque de código para instalar cualquier paquete faltante:

# Creating the list to install
pkgs <- c(
  "ergm", "sna", "igraph", "intergraph", "netplot", "netdiffuseR", "rgexf"
  )

# Checking if we can load them and install them if not available
for (pkg in pkgs) {
  if (!require(pkg, character.only = TRUE)) {

    # If not present, will install it
    install.packages(pkg, character.only = TRUE)

    # And load it!
    library(pkg, character.only = TRUE)

  }
}

Una versión grabada está disponible aquí.

Modelos de Grafos Aleatorios

Aunque hay toneladas de datos de redes sociales, utilizaremos uno artificial para este capítulo. Hacemos esto ya que siempre es útil tener más ejemplos simulando redes aleatorias. Para este capítulo, clasificaremos los modelos de grafos aleatorios para muestrear y generar redes en tres categorías:

Exógenos: Grafos donde la estructura está determinada por una regla macro, ej., densidad esperada, distribución de grados, o secuencia de grados. En estos casos, los enlaces se asignan para cumplir con una macro-propiedad.
Endógenos: Esta categoría incluye todos los Grafos Aleatorios generados basándose en información endógena, ej., mundo pequeño, libre de escala, etc. Aquí, una regla de creación de enlaces da origen a una macro propiedad, por ejemplo, apego preferencial en redes libres de escala.
Modelos Exponenciales de Grafos Aleatorios: En general, dado que los ERGMs componen una familia de modelos estadísticos, siempre (o casi siempre) podemos encontrar una especificación de modelo que coincida con las categorías anteriores. Ya sea que estemos pensando en secuencia de grados, apego preferencial, o una mezcla de ambos, los ERGMs pueden ser la línea base para cualquiera de esos modelos.

Los últimos, ERGMs, son una generalización que cubre todas las clases. Debido a eso, utilizaremos ERGMs para generar nuestra red artificial.

Redes Sociales en Escuelas

Un tipo común de red que analizamos son las redes de amistad. En este caso, utilizaremos ERGMs para simular redes de amistad dentro de una escuela. En nuestro mundo simulado, estas redes estarán dominadas por los siguientes fenómenos:

Baja densidad,
Homofilia racial,
Balance estructural,
Y homofilia de edad.

Si has estado prestando atención a los capítulos anteriores, notarás que, de estas cinco propiedades, solo una constituye grafos de Markov. Dentro de un enlace, la homofilia y la densidad solo dependen del ego y el alter. En la homofilia racial, solo importa la raza del ego y del alter para la formación del enlace, pero, en el caso del Balance estructural, el ego es más probable que se haga amigo del alter si un amigo del ego es amigo del alter, es decir, “el amigo de mi amigo es mi amigo.”

Los pasos de simulación son los siguientes:

Sortear una población de n estudiantes y distribuir aleatoriamente raza y edad entre ellos.
Crear un objeto network.
Simular los enlaces en la red vacía.

Aquí está el código:

set.seed(712)
n <- 200

# Step 1: Students
race   <- sample(c("white", "non-white"), n, replace = TRUE)
age    <- sample(c(10, 14, 17), n, replace = TRUE)

# Step 2: Create an empty network
library(ergm)
library(network)
net <- network.initialize(n)

net %v% "race"   <- race
net %v% "age"    <- age

# Step 3: Simulate a graph
net_sim <- simulate(
    net ~ edges +
    nodematch("race") +
    ttriad +
    absdiff("age"),
    coef = c(-4, .5, .25, -.5)
    )

¿Qué acaba de pasar? Aquí hay un desglose línea por línea:

set.seed(712) Dado que esta es una simulación aleatoria, necesitamos fijar una semilla para que sea reproducible. De otra manera, los resultados cambiarían con cada iteración.
n <- 200 Estamos asignando el valor 200 al objeto n. Esto hará las cosas más fáciles ya que, si es necesario, cambiar el tamaño de las redes puede hacerse en la parte superior del código.
race <- sample(c("white", "non-white"), n, replace = TRUE) Estamos muestreando 200, o en realidad, n valores del vector c("white", "non-white") con reemplazo.
age <- sample(c(10, 14, 17), n, replace = TRUE) ¡Lo mismo que antes, pero con edades!
library(ergm) ¡Cargando el paquete de R ergm, que necesitamos para simular las redes!
library(network) Cargando el paquete de R network, que necesitamos para crear el grafo vacío.
net <- network.initialize(n) Creando un grafo vacío de tamaño n.
net %v% "race" <- race Usando el operador %v%, podemos acceder a las características de los vértices en el objeto red. Dado que race no existe en la red aún, el operador simplemente la crea. Nota que el número de vértices coincide con la longitud del vector race.
net %v% "age" <- age ¡Lo mismo que con race!
net_sim <- simulate( ¡Simulando un ERGM! Un par de observaciones aquí:
1. El LHS (lado izquierdo) de la ecuación tiene la red, net
2. El RHS (lo adivinaste) tiene los términos que gobiernan el proceso.
3. Para baja densidad, usamos el término edges con un -4.0 correspondiente para el parámetro.
4. Para homofilia racial, usamos el nodematch("race") con un valor de parámetro correspondiente de 0.5.
5. Para balance estructural, usamos el término ttriad con parámetro 0.25.
6. Para homofilia de edad, usamos el término absdiff("age") con parámetro -0.5. Esto es, en rigor, un término que captura heterofilia. No obstante, la heterofilia es lo opuesto a la homofilia.

Echemos un vistazo rápido al grafo resultante:

library(sna)
gplot(net_sim)

¡Ahora podemos empezar a ver si obtuvimos lo que queríamos! Antes de eso, guardemos la red como un archivo de texto plano para que podamos practicar leyendo redes de vuelta en R!

write.csv(
  x         = as.edgelist(net_sim),
  file      = "06-edgelist.csv",
  row.names = FALSE
  )

write.csv(
  x         = as.data.frame(net_sim, unit = "vertices"),
  file      = "06-nodes.csv",
  row.names = FALSE
  )

Leyendo una red

El primer paso para analizar datos de red es leerlos. Muchas veces encontrarás datos en forma de una matriz de adyacencia. Otras veces, los datos vendrán en forma de una lista de enlaces. Otro formato común es la lista de adyacencia, que es una versión comprimida de una lista de enlaces. Veamos cómo se ven los formatos para la siguiente red:

example_graph <- matrix(0L, 4, 4, dimnames = list(letters[1:4], letters[1:4]))
example_graph[c(2, 7)] <- 1L
example_graph["c", "d"] <- 1L
example_graph["d", "c"] <- 1L
example_graph <- as.network(example_graph)
set.seed(1231)
gplot(example_graph, label = letters[1:4])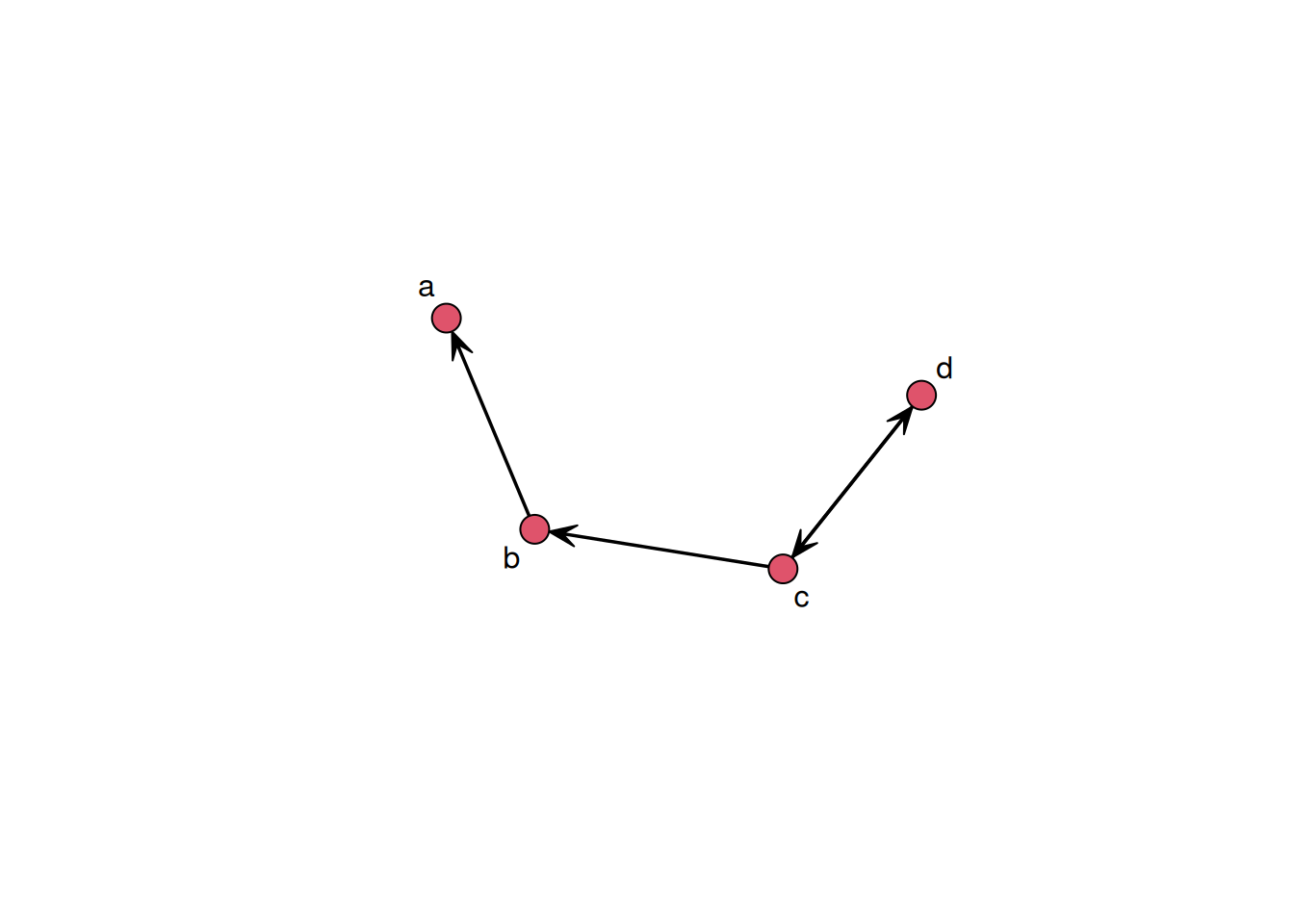

Matriz de adyacencia una matriz de tamaño n por n donde la entrada ij-ésima representa el enlace entre i y j. En una red dirigida, decimos que i se conecta a j, por lo que la i-ésima fila muestra los enlaces que i envía al resto de la red. De igual manera, en un grafo dirigido, la j-ésima columna muestra los enlaces enviados a j. Para grafos no dirigidos, la matriz de adyacencia es usualmente diagonal superior o inferior. La matriz de adyacencia de un grafo no dirigido es simétrica, por lo que no necesitamos reportar la misma información dos veces. Por ejemplo:

as.matrix(example_graph)

Lista de enlaces una matriz de tamaño |E| por 2, donde |E| es el número de enlaces. Cada entrada representa un enlace en el grafo.

as.edgelist(example_graph)

     [,1] [,2]
[1,]    2    1
[2,]    3    2
[3,]    3    4
[4,]    4    3
attr(,"n")
[1] 4
attr(,"vnames")
[1] "a" "b" "c" "d"
attr(,"directed")
[1] TRUE
attr(,"bipartite")
[1] FALSE
attr(,"loops")
[1] FALSE
attr(,"class")
[1] "matrix_edgelist" "edgelist"        "matrix"          "array"

El comando convierte el objeto network en una matriz con un conjunto de atributos (que también se imprimen.)

Lista de adyacencia Este formato de datos usa menos espacio que las listas de enlaces ya que los enlaces se agrupan por ego (fuente.)

igraph::as_adj_list(intergraph::asIgraph(example_graph))

[[1]]
+ 1/4 vertex, from a87c16b:
[1] 2

[[2]]
+ 2/4 vertices, from a87c16b:
[1] 1 3

[[3]]
+ 3/4 vertices, from a87c16b:
[1] 2 4 4

[[4]]
+ 2/4 vertices, from a87c16b:
[1] 3 3

La función igraph::as_adj_list convierte el objeto igraph en una lista de tipo lista de adyacencia. En texto plano se vería algo así:

Aquí trataremos con una lista de enlaces que incluye información de nodos. En mi opinión, esta es una de las mejores maneras de compartir datos de red. Leamos los datos en R usando la función read.csv:

edges <- read.csv("06-edgelist.csv")
nodes <- read.csv("06-nodes.csv")

Ahora tenemos dos objetos de clase data.frame, edges y nodes. Inspeccionémoslos usando la función head:

head(edges)

head(nodes)

  vertex.names      race age
1            1 non-white  10
2            2     white  10
3            3     white  17
4            4 non-white  14
5            5 non-white  17
6            6 non-white  14

Siempre es importante mirar los datos antes de crear la red. La mayoría de errores comunes ocurren antes de leer los datos y podrían pasar desapercibidos en muchos casos. Algunos ejemplos:

Los encabezados en el archivo podrían ser tratados como datos, o los archivos pueden no tener encabezados.
Las columnas Ego/alter pueden aparecer en el orden incorrecto. Tanto los paquetes igraph como network toman la primera y segunda columnas de las listas de enlaces como ego y alter.
Los aislados, que no aparecerían en la lista de enlaces, pueden estar faltando del conjunto de información de nodos. Este es uno de los errores más comunes.
Los nodos que aparecen en la lista de enlaces pueden estar faltando de la lista de nodos.

Tanto igraph como network tienen funciones para leer listas de enlaces con una lista de nodos correspondiente; las funciones graph_from_data_frame y as.network, respectivamente. Aunque, para ambos casos, puedes evitar usar una lista de nodos, es altamente recomendado ya que entonces (a) te asegurarás de que los aislados estén incluidos y (b) te darás cuenta de posibles problemas en los datos. Un error frecuente en graph_from_data_frame es nodos presentes en la lista de enlaces pero no en el conjunto de nodos.

net_ig <- igraph::graph_from_data_frame(
  d        = edges,
  directed = TRUE,
  vertices = nodes
)

Usando as.network del paquete network:

net_net <- network::as.network(
  x        = edges,
  directed = TRUE,
  vertices = nodes
)

Como puedes ver, ambas sintaxis son muy similares. El punto principal aquí es que mientras más explícitos seamos, mejor. Sin embargo, R puede ser brillante; ser tímido, es decir, no lanzar advertencias o errores, no es poco común. En la siguiente sección, finalmente comenzaremos a visualizar los datos.

Visualizando la red

Nos enfocaremos en tres atributos diferentes que podemos usar para esta visualización: Tamaño de nodo, forma de nodo, y color de nodo. Aunque no hay reglas particulares, algunas ideas que puedes seguir son:

Tamaño de nodo Úsalo para describir una medición continua. Esta característica se usa a menudo para destacar nodos importantes, ej., usando una de las muchas mediciones de grado disponibles.
Forma de nodo Las formas pueden usarse para representar valores categóricos. Una buena figura no presentará demasiadas de ellas; menos de cuatro tendría sentido.
Color de nodo Como las formas, los colores pueden usarse para representar valores categóricos, por lo que aplica la misma idea. Además, no es loco usar tanto forma como color para representar la misma característica.

Nota que no hemos hablado de algoritmos de diseño. Los paquetes de R para construir grafos usualmente tienen reglas internas para decidir qué algoritmo usar. Discutiremos eso más adelante. Empecemos por tamaño.

Tamaño de vértice

Encontrar la escala correcta puede ser algo difícil. Dibujaremos el grafo cuatro veces para ver qué tamaño sería el mejor:

# Sized by indegree
net_sim %v% "indeg" <- sna::degree(net_sim, cmode = "indegree")

# Changing device config
op <- par(mfrow = c(2, 2), mai = c(.1, .1, .1, .1))

# Plotting
glayout <- gplot(net_sim, vertex.cex = (net_sim %v% "indeg") * 2)
gplot(net_sim, vertex.cex = net_sim %v% "indeg", coord = glayout)
gplot(net_sim, vertex.cex = (net_sim %v% "indeg")/2, coord = glayout)
gplot(net_sim, vertex.cex = (net_sim %v% "indeg")/10, coord = glayout)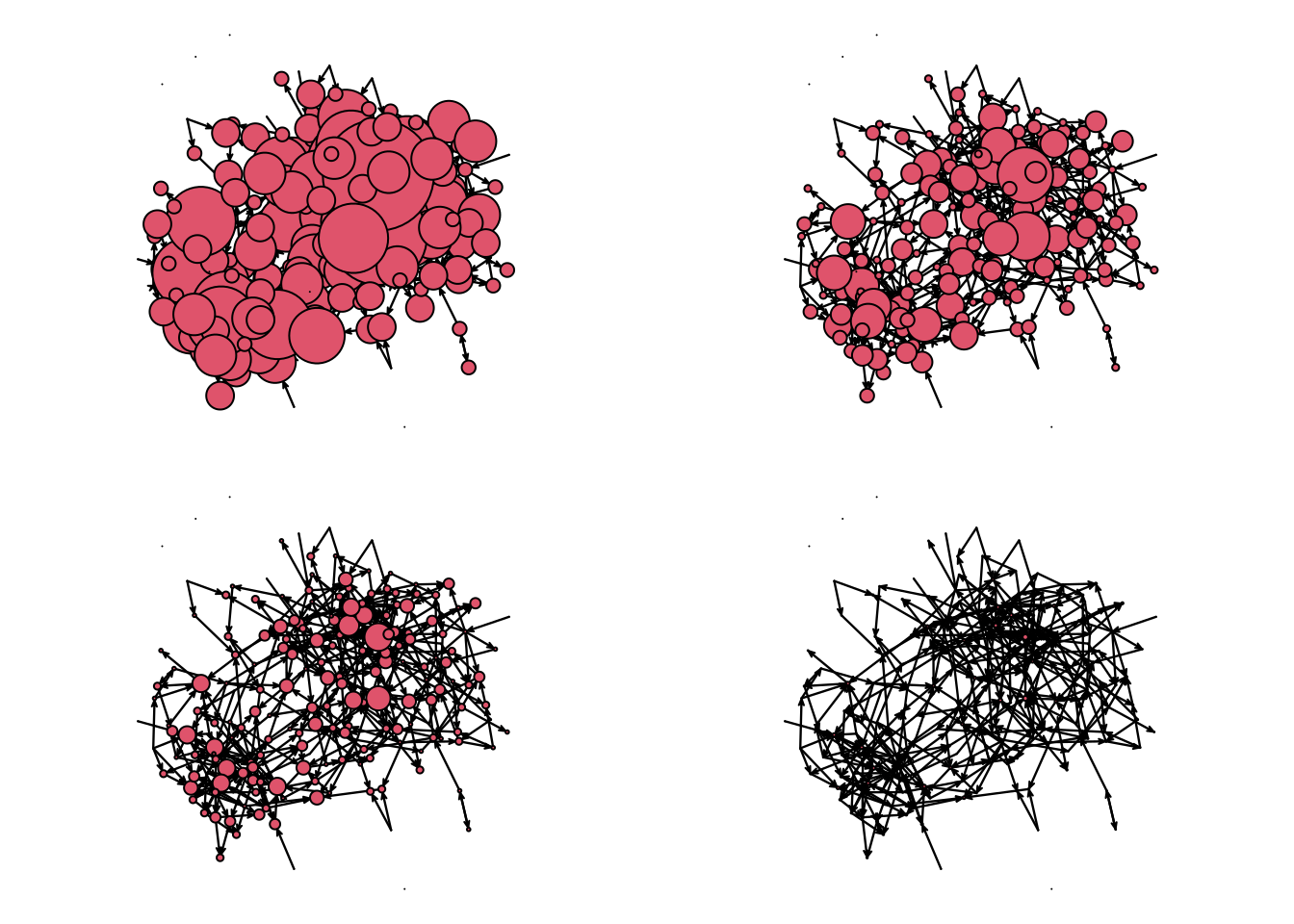

# Restoring device config
par(op)

Línea por línea hicimos lo siguiente:

net_sim %v% "indeg" <- degree(net_sim, cmode = "indegree") Creamos un nuevo atributo de vértice llamado indegree y lo asignamos al objeto red. El indegree se calcula usando la función degree del paquete sna. Dado que igraph también tiene una función degree, nos estamos asegurando de que R use la de sna y no la de igraph. La notación package::function es útil para estos casos.
op <- par(mfrow = c(2, 2), mai = c(.1, .1, .1, .1)) Esto cambia la información del dispositivo gráfico a (a) mfrow = c(2,2) tener una cuadrícula 2x2 por fila, significando que las nuevas figuras se agregarán de izquierda a derecha y luego de arriba a abajo, y (b) establecer los márgenes en la figura para que sean 0.1 pulgadas en los cuatro tamaños.
glayout <- gplot(net_sim, vertex.cex = (net_sim %v% "indeg") * 2) generando la gráfica y registrando el diseño. La función gplot devuelve una matriz de tamaño # vertices por 2 con las posiciones de los vértices. También estamos pasando el argumento vertex.cex, que usamos para especificar el tamaño de cada vértice. En nuestro caso, decidimos dimensionar los vértices proporcional a su indegree por dos.
gplot(net_sim, vertex.cex = net_sim %v% "indeg", coord = glayout), nuevamente, estamos dibujando el grafo usando las coordenadas del dibujo anterior, pero ahora los vértices son la mitad del tamaño de la figura original.

Las otras dos llamadas son similares a la cuatro. Si usáramos igraph, establecer el tamaño puede ser más accesible gracias al paquete de R netdiffuseR. Comencemos convirtiendo nuestra red a un objeto igraph con el paquete de R intergraph.

library(intergraph)
library(igraph)

# Converting the network object to an igraph object
net_sim_i <- asIgraph(net_sim)

# Plotting with igraph
plot(
  net_sim_i,
  vertex.size = netdiffuseR::rescale_vertex_igraph(
    vertex.size = V(net_sim_i)$indeg,
    minmax.relative.size = c(.01, .1)
  ), 
  layout       = glayout,
  vertex.label = NA
)

También podríamos haber probado netplot, que debería hacer las cosas más fáciles y hacer un mejor uso del espacio:

library(netplot)
nplot(
  net_sim, layout = glayout,
  vertex.color = "tomato",
  vertex.frame.color = "darkred"
  )

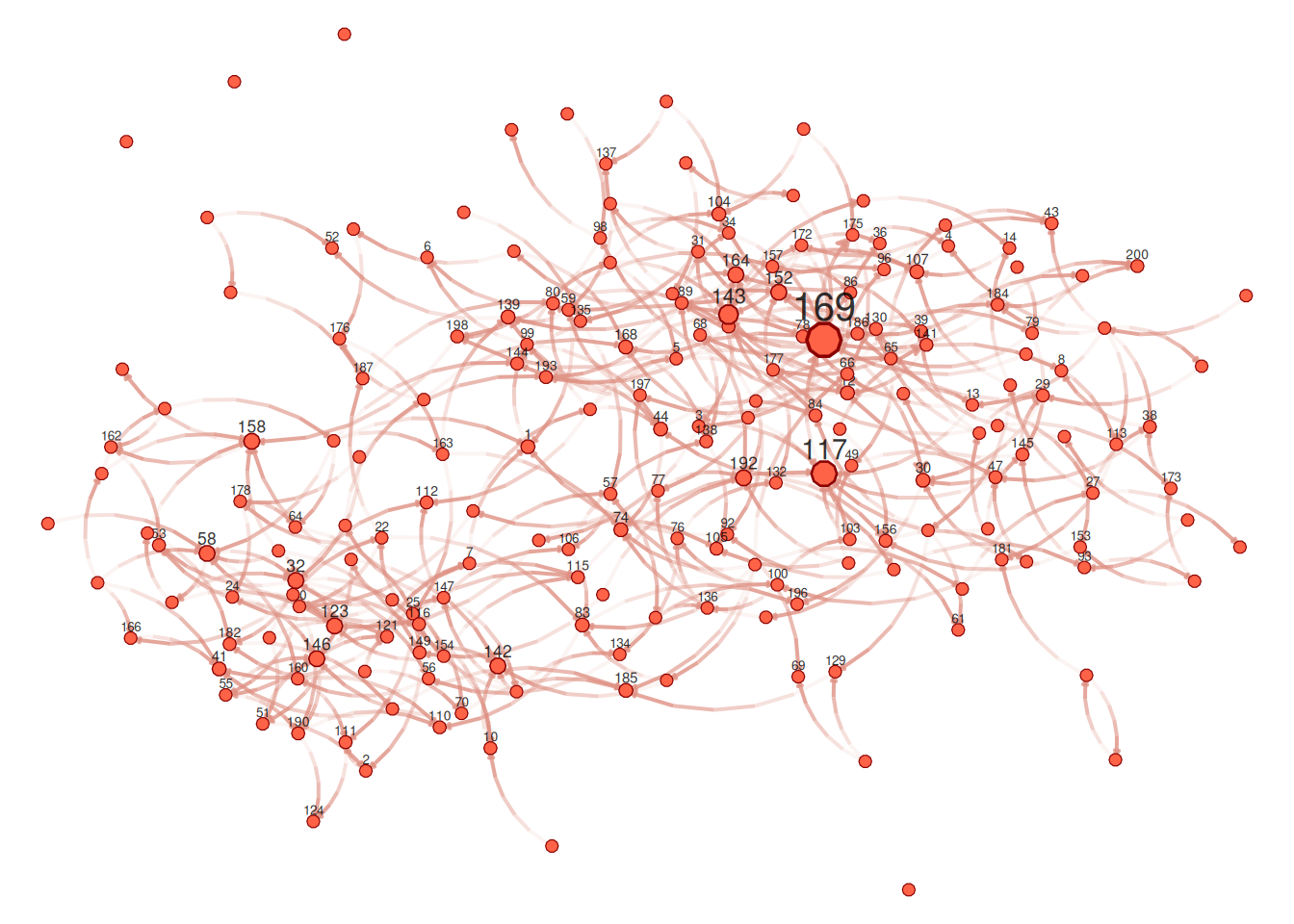
Con una buena idea para el tamaño, ahora podemos empezar a mirar el color de vértice.

Color de vértice

Para el color, usaremos la edad del vértice. Aunque la edad es, por definición, continua, solo tenemos tres valores para la edad. Debido a esto, podemos tratar la edad como categórica. En lugar de usar nplot iremos adelante con nplot_base. En esta versión del libro, el paquete netplot no tiene una manera fácil de agregar leyendas con la función central, nplot; por lo tanto, usamos nplot_base que es compatible con la función de R legend, como veremos ahora:

# Specifying colors for each vertex
vcolors_palette <- c("10" = "gray", "14" = "tomato", "17" = "steelblue")
vcolors <- vcolors_palette[as.character(net_sim %v% "age")]
net_sim %v% "color" <- vcolors

# Plotting
nplot_base(
  net_ig,
  layout = glayout,
  vertex.color = net_sim %v% "color",
  )

# Color legend
legend(
  "bottomright",
  legend = names(vcolors_palette),
  fill   = vcolors_palette, 
  bty    = "n",
  title  = "Age"
  )

Línea por línea, esto es lo que acabamos de hacer:

vcolors <- c("10" = "gray", "14" = "tomato", "17" = "steelblue") creamos un vector de caracteres con tres elementos, "gray", "tomato", y "blue". Además, el vector tiene nombres asignados, "10", "14", y "17"– las edades que tenemos en la red–para que podamos acceder a sus elementos indexando por nombre, ej., si escribimos vcolors["10"] R devuelve el valor "gray".
vcolors <- vcolors[as.character(net_sim %v% "age")] hay varias cosas pasando en esta línea. Primero, extraemos el atributo “age” de la red usando el operador %v%. Luego transformamos el vector resultante de tipo entero a tipo carácter con la función as.character. Finalmente, usando el vector de caracteres resultante con valores "10", "14", "17", ..., recuperamos valores de vcolors indexando por nombre. El vector resultante es de longitud igual al conteo de vértices en la red.
net_sim %v% "color" <- vcolors crea un nuevo atributo de vértice, color. El valor asignado es el resultado de hacer subset de vcolors por las edades de cada vértice.
nplot_base(... finalmente dibuja la red. Pasamos las coordenadas de vértice previamente computadas y los colores de vértice con el nuevo atributo color.
legend(...) Veamos un parámetro a la vez:
1. "bottomright" dice la posición general de la leyenda
2. legend = names(vcolors) pasa la leyenda actual (texto); en nuestro caso las edades de individuos.
3. fill = vcolors pasa los colores asociados con el texto.
4. bty = "n" suprime envolver la leyenda dentro de una caja.
5. title = "Age" establece el título como “Age”.

Forma de vértice

Para la forma, usaremos la raza del vértice. Aunque la raza es, por definición, categórica, solo tenemos dos valores para la raza. Debido a esto, podemos tratar la raza como categórica.

# Specifying the shapes for each vertex
vshape_list <- c("white" = 15, "non-white" = 3)
vshape      <- vshape_list[as.character(net_sim %v% "race")]
net_sim %v% "shape" <- vshape

# Plotting
nplot_base(
  net_ig,
  layout = glayout,
  vertex.color = net_sim %v% "color",
  vertex.nsides = net_sim %v% "shape"
  )

# Color legend
legend(
  "bottomright",
  legend = names(vcolors_palette),
  fill   = vcolors_palette, 
  bty    = "n",
  title  = "Age"
  )

# Shape legend
legend(
  "bottomleft",
  legend = names(vshape_list),
  pch    = c(1, 2), 
  bty    = "n",
  title  = "Race"
  )

Ahora comparemos la figura con nuestro ERGM original:

Baja densidad (edges) Sin baja densidad, la figura sería una maraña de cabello.
Homofilia racial (nodematch("race")) Aunque no sorprendentemente evidente, los nodos tienden a formar pequeños grupos por forma, que, en nuestro modelo, representa raza.
Balance estructural (ttriad) Una fuerza, en este caso, opuesta a la baja densidad, mayor prevalencia de triadas transitivas hace que los individuos se agrupen.
Homofilia de edad (absdiff("age")) Esta es la característica más prominente del grafo. En él, los nodos se agrupan por edad.

De las cuatro características, homofilia de edad es la que se destaca. ¿Por qué es este el caso? Si miramos nuevamente los parámetros usados en el ERGM y cómo estos interactúan con los atributos de los vértices, encontraremos la respuesta:

Las log-odds de un nuevo enlace racialmente homofílico son 1\times\theta_{\text{race-homophily}} = 0.5.
Pero, las log-odds de un enlace heterofílico de edad entre, digamos, jóvenes de 14 y 17 años es |17-14|\theta_{\text{age-homophily}} = 3\times -0.5 = -1.5.
Por lo tanto, el efecto de heterofilia (que es justo lo opuesto a homofilia) es significativamente mayor, en realidad tres veces en este caso, que el efecto de homofilia racial.

Esta observación se vuelve clara si ejecutamos otra simulación con la misma semilla, pero ajustando para el tamaño máximo que el efecto de homofilia de edad puede tomar. Una manera rápida y sucia de lograr esto es re-ejecutar la simulación con el término nodematch en lugar del término absdiff. De esta manera, (a) explícitamente operacionalizamos el término como homofilia (antes era heterofilia,) y (b) tenemos ambos efectos de homofilia con la misma influencia en el modelo:

net_sim2 <- simulate(
    net ~ edges +
    nodematch("race") +
    ttriad +
    nodematch("age"),
    coef = c(-5, .5, .25, .5) # This line changed
    )

Re-haciendo la gráfica. Del dibujo de grafo anterior, solo la estructura del grafo cambió. Los atributos de vértice son los mismos por lo que podemos ir adelante y re-usarlos. Como mencioné anteriormente, la función nplot_base actualmente soporta objetos igraph, por lo que usaremos intergraph::asIgraph para que funcione:

# Plotting
nplot_base(
  asIgraph(net_sim2),
  # We comment this out to allow for a new layout
  # layout = glayout, 
  vertex.color = net_sim %v% "color",
  vertex.nsides = net_sim %v% "shape"
  )

# Color legend
legend(
  "bottomright",
  legend = names(vcolors_palette),
  fill   = vcolors_palette, 
  bty    = "n",
  title  = "Age"
  )

# Shape legend
legend(
  "bottomleft",
  legend = names(vshape_list),
  pch    = c(1, 2), 
  bty    = "n",
  title  = "Race"
  )

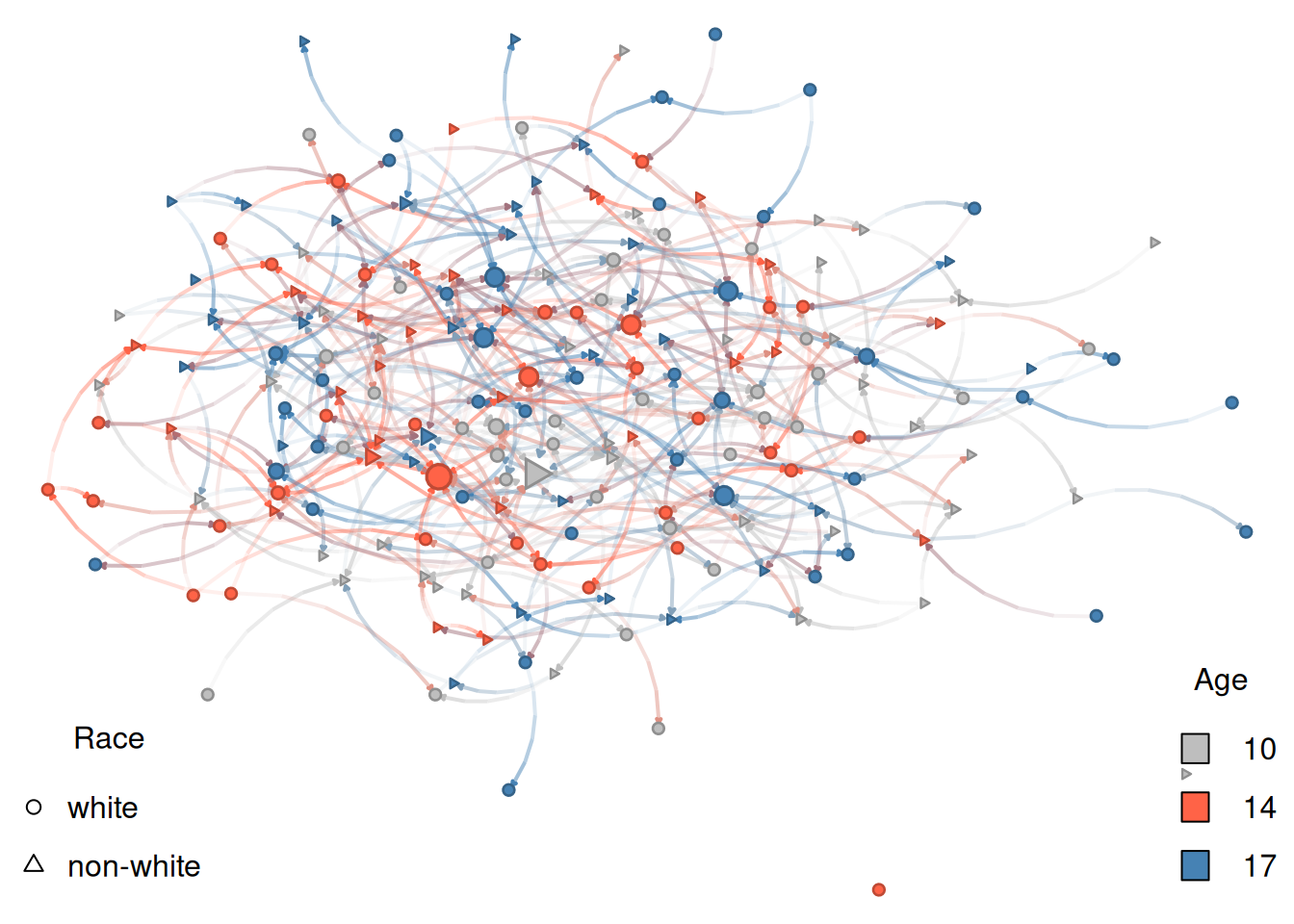
Como se esperaba, ya no hay un efecto dominante en homofilia. Una cosa importante que podemos aprender de este ejemplo final es que los fenómenos no siempre se mostrarán en la visualización de grafos. Un análisis cuidadoso en redes complejas es imprescindible.