Comportamiento y coevolución

Published

September 7, 2024

Modified

September 7, 2025

Nota de Traducción

Esta versión del capítulo fue traducida de manera automática utilizando IA. El capítulo aún no ha sido revisado por un humano.

Note

Todo el contenido de esta sección fue presentado durante la Escuela de Verano Sistemas Complejos 2024 en la Universidad del Desarrollo. La versión original se puede encontrar aquí.

Introducción

Esta sección se enfoca en la inferencia que involucra redes y un resultado secundario. Aunque hay muchas formas de estudiar la coevolución o dependencia entre red y comportamiento, esta sección se enfoca en dos clases de análisis: cuando la red es fija y cuando tanto la red como el comportamiento se influyen mutuamente.

Si tratamos la red como dada o endógena establece la complejidad de realizar inferencia estadística. El análisis de datos se vuelve mucho más directo si nuestra investigación se enfoca en resultados a nivel individual embebidos en una red y no en la red misma. Aquí, trataremos con tres casos particulares: (1) cuando los efectos de red son rezagados, (2) redes egocéntricas, y (3) cuando los efectos de red son contemporáneos.

Exposición rezagada

Si asumimos que la influencia de la red en forma de exposición está rezagada, tenemos uno de los casos más directos para la inferencia de redes (Haye et al. 2019; Valente and Vega Yon 2020; Valente, Wipfli, and Vega Yon 2019). Aquí, en lugar de tratar con modelos estadísticos complicados, el problema se reduce a estimar un modelo de regresión lineal simple. Generalmente, los efectos de exposición rezagada se ven así:

y_{it} = \rho \left(\sum_{j\neq i}X_{ij}\right)^{-1}\left(\sum_{j\neq i}y_{jt-1} X_{ij}\right) + {\bm{{\theta}}}^{\mathbf{t}}\bm{{w_i}} + \varepsilon,\quad \varepsilon \sim \text{N}(0, \sigma^2)

donde y_{it} es el resultado del individuo i en el tiempo t, X_{ij} es la entrada ij-ésima de la matriz de adyacencia, \bm{{\theta}} es un vector de coeficientes, \bm{{w_i}} es un vector de características/covariables del individuo i, y \varepsilon_i es un error distribuido normalmente. Aquí, el componente clave es \rho: el coeficiente asociado con el efecto de exposición de red.

La estadística de exposición, \left(\sum_{j\neq i}X_{ij}\right)^{-1}\left(\sum_{j\neq i}y_{jt-1} X_{ij}\right), es el promedio ponderado de los resultados de los vecinos de i en el tiempo t-1.

Ejemplo de código: Exposición rezagada

El siguiente ejemplo de código muestra cómo estimar un efecto de exposición rezagada usando la función glm en R. El modelo que simularemos y estimaremos presenta un grafo de Bernoulli con 1,000 nodos y una densidad de 0.01.

y_{it} = \theta_1 + \rho \text{Exposure}_{i,t-1} + \theta_2 w_i + \varepsilon

donde \text{Exposure}_{i,t-1} es la estadística de exposición definida arriba, y w_i es un vector de covariables.

## Simulando datos
n <- 1000
time <- 2
theta <- c(-1, 3)

## Muestreando una red de Bernoulli
set.seed(3132)
p <- 0.01
X <- matrix(rbinom(n^2, 1, p), nrow = n)
diag(X) <- 0

## Covariable
W <- matrix(rnorm(n), nrow = n)

## Simulando el resultado
rho <- 0.5
Y0 <- cbind(rnorm(n))

## La exposición rezagada
expo <- (X %*% Y0)/rowSums(X)
Y1 <- theta[1] + rho * expo + W * theta[2] + rnorm(n)

Ahora ajustamos el modelo usando GLM, en este caso, regresión lineal

fit <- glm(Y1 ~ expo + W, family = "gaussian")
summary(fit)


Call:
glm(formula = Y1 ~ expo + W, family = "gaussian")

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) -1.07187    0.03284 -32.638  < 2e-16 ***
expo         0.61170    0.10199   5.998  2.8e-09 ***
W            3.00316    0.03233  92.891  < 2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

(Dispersion parameter for gaussian family taken to be 1.071489)

    Null deviance: 10319.3  on 999  degrees of freedom
Residual deviance:  1068.3  on 997  degrees of freedom
AIC: 2911.9

Number of Fisher Scoring iterations: 2

Redes egocéntricas

Generalmente, cuando usamos redes egocéntricas y resultados de los egos, estamos pensando en un modelo donde una observación es el par (y_i, X_i), esto es, el resultado del individuo i y la red egocéntrica del individuo i. Cuando tal es el caso, dado que (a) las redes son independientes entre egos y (b) las redes son fijas, como el caso anterior, un modelo de regresión lineal simple es suficiente para realizar los análisis. Un modelo típico se ve así:

\bm{{y}} = \bm{{\theta}}_{x}^{\mathbf{t}}s(\bm{{X}}) + \bm{{\theta}}^{\mathbf{t}}\bm{{w}} + \varepsilon,\quad \varepsilon \sim \text{N}(0, \sigma^2)

Donde \bm{{y}} es un vector de resultados, \bm{{X}} es una matriz de redes egocéntricas, \bm{{w}} es un vector de covariables, \bm{{\theta}} es un vector de coeficientes, y \varepsilon es un vector de errores. El componente clave aquí es s(\bm{{X}}), que es un vector de estadísticas suficientes de las redes egocéntricas. Por ejemplo, si estamos interesados en el número de vínculos, s(\bm{{X}}) es un vector del número de vínculos de cada ego.

Ejemplo de código: Redes egocéntricas

Para este ejemplo, simularemos un flujo de 1,000 grafos de Bernoulli analizando la probabilidad de deserción escolar. Cada red tendrá entre 4 y 10 nodos y tendrá una densidad de 0.4. El proceso de generación de datos es el siguiente:

{\Pr{}}_{\bm{{\theta}}}\left(Y_i=1\right) = \text{logit}^{-1}\left(\bm{{\theta}}_x s(\bm{{X}}_i) \right)

Donde s(X) \equiv \left(\text{densidad}, \text{n vínculos mutuos}\right), y \bm{{\theta}}_x = (0.5, -1). Este modelo solo presenta estadísticas suficientes. Comenzamos simulando las redes

set.seed(331)
n <- 1000
sizes <- sample(4:10, n, replace = TRUE)

## Simulando las redes
X <- lapply(sizes, function(x) matrix(rbinom(x^2, 1, 0.4), nrow = x))
X <- lapply(X, \(x) {diag(x) <- 0; x})

## Inspeccionando las primeras 5
head(X, 5)

[[1]]
     [,1] [,2] [,3] [,4] [,5]
[1,]    0    1    1    1    0
[2,]    0    0    0    0    0
[3,]    0    1    0    0    0
[4,]    0    0    0    0    0
[5,]    1    0    0    1    0

[[2]]
     [,1] [,2] [,3] [,4]
[1,]    0    0    0    0
[2,]    0    0    0    0
[3,]    0    0    0    0
[4,]    1    0    1    0

[[3]]
     [,1] [,2] [,3] [,4] [,5] [,6]
[1,]    0    1    0    1    0    0
[2,]    0    0    0    0    0    0
[3,]    0    1    0    0    0    1
[4,]    0    0    0    0    1    0
[5,]    0    0    0    0    0    0
[6,]    0    0    0    0    0    0

[[4]]
     [,1] [,2] [,3] [,4] [,5]
[1,]    0    1    0    1    0
[2,]    0    0    0    0    1
[3,]    0    1    0    0    0
[4,]    0    1    1    0    1
[5,]    1    0    1    0    0

[[5]]
     [,1] [,2] [,3] [,4] [,5]
[1,]    0    0    0    0    0
[2,]    1    0    0    0    0
[3,]    1    0    0    0    0
[4,]    0    0    0    0    0
[5,]    1    0    0    0    0

Usando el paquete de R ergm (Handcock et al. 2023; Hunter et al. 2008), podemos extraer las estadísticas suficientes asociadas de las redes egocéntricas:

library(ergm)
stats <- lapply(X, \(x) summary_formula(x ~ density + mutual))

## Convirtiendo la lista en una matriz
stats <- do.call(rbind, stats)

## Inspeccionando las primeras 5
head(stats, 5)

       density mutual
[1,] 0.3000000      0
[2,] 0.1666667      0
[3,] 0.1666667      0
[4,] 0.4500000      0
[5,] 0.1500000      0

Ahora simulamos los resultados

y <- rbinom(n, 1, plogis(stats %*% c(0.5, -1)))
glm(y ~ stats, family = binomial(link = "logit")) |>
  summary()


Call:
glm(formula = y ~ stats, family = binomial(link = "logit"))

Coefficients:
             Estimate Std. Error z value Pr(>|z|)    
(Intercept)   0.07319    0.41590   0.176    0.860    
statsdensity  0.42568    1.26942   0.335    0.737    
statsmutual  -1.14804    0.12166  -9.436   <2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

(Dispersion parameter for binomial family taken to be 1)

    Null deviance: 768.96  on 999  degrees of freedom
Residual deviance: 518.78  on 997  degrees of freedom
AIC: 524.78

Number of Fisher Scoring iterations: 7

Los efectos de red son endógenos

Aquí tenemos dos enfoques diferentes: Autocorrelación Espacial [SAR], y el modelo de atributo de actor autologístico [ALAAM] (Robins, Pattison, and Elliott 2001). El primero es una generalización del modelo de regresión lineal que considera la dependencia espacial. El segundo es un pariente cercano de los ERGMs que trata las covariables como endógenas y la red como exógena. En general, los ALAAMs son más flexibles que los SARs, pero los SARs son más fáciles de estimar.

SAR Formalmente, los modelos SAR (ver LeSage 2008) pueden usarse para estimar efectos de exposición de red. La forma general es:

\bm{{y}} = \rho \bm{{W}} \bm{{y}} + \bm{{\theta}}^{\mathbf{t}} \bm{{X}} + \epsilon,\quad \epsilon \sim \text{MVN}(0, \Sigma)

donde \bm{{y}}\equiv \{y_i\} es un vector de resultados, \rho es un coeficiente de autocorrelación, \bm{{W}} \in \{w_{ij}\} es una matriz cuadrada estocástica por filas de tamaño n, \bm{{\theta}} es un vector de parámetros del modelo, \bm{{X}} es la matriz correspondiente con variables exógenas, y \epsilon es un vector de errores que se distribuye normal multivariado con media 0 y covarianza \Sigma.[^notation] El modelo SAR es una generalización del modelo de regresión lineal que considera la dependencia espacial. El modelo SAR puede estimarse usando el paquete spatialreg en R (Roger Bivand 2022).

Tip

¿Cuál es la red apropiada para usar en el modelo SAR? Según LeSage and Pace (2014), no es muy importante. Dado que (I_n - \rho \mathbf{W})^{-1} = \rho \mathbf{W} + \rho^2 \mathbf{W}^2 + \dots.

Aunque el modelo SAR fue desarrollado para datos espaciales, es fácil aplicarlo a datos de red. Además, cada entrada del vector \bm{{Wy}} tiene la misma definición que la exposición de red, es decir

\bm{{Wy}} \equiv \left\{\sum_{j}y_j w_{ij}\right\}_i

Dado que \bm{{W}} es estocástica por filas, \bm{{Wy}} es un promedio ponderado del resultado de los vecinos de i, es decir, un vector de exposiciones de red.

ALAAM La forma más simple en que podemos pensar sobre esta clase de modelos es como si una covariable dada intercambiara lugares con la red en un ERGM, entonces la red ahora es fija y la covariable es la variable aleatoria. Aunque los ALAAMs también pueden estimar efectos de exposición de red, podemos usarlos para construir modelos más complejos más allá de la exposición. La forma general es:

{\mathbb{P}\left({\bm{{Y}} = \bm{{y}}}\vphantom{\bm{{W}},\bm{{X}}}\;\right|\left.\vphantom{\bm{{Y}} = \bm{{y}}}{\bm{{W}},\bm{{X}}}\right)} = \text{exp}\left\{\left(\bm{{\theta}}^{\mathbf{t}}s(\bm{{y}},\bm{{W}}, \bm{{X}})\right)\right\}\times\eta(\bm{{\theta}})^{-1}

\eta(\bm{{\theta}}) = \sum_{\bm{{y}}}\text{exp}\left\{\left(\bm{{\theta}}^{\mathbf{t}}s(\bm{{y}},\bm{{W}}, \bm{{X}})\right)\right\}

Donde \bm{{Y}}\equiv \{y_i \in (0, 1)\} es un vector de resultados individuales binarios, \bm{{W}} denota la red social, \bm{{X}} es una matriz de variables exógenas, \bm{{\theta}} es un vector de parámetros del modelo, s(\bm{{y}},\bm{{W}}, \bm{{X}}) es un vector de estadísticas suficientes, y \eta(\bm{{\theta}}) es una constante normalizadora.

Ejemplo de código: SAR

La simulación de modelos SAR puede hacerse usando la siguiente observación: Aunque el resultado aparece en ambos lados de la ecuación, podemos aislarlo en un lado y resolverlo; formalmente:

\bm{{y}} = \rho \bm{{X}} \bm{{y}} + \bm{{\theta}}^{\mathbf{t}}\bm{{W}} + \varepsilon \implies \bm{{y}} = \left(\bm{{I}} - \rho \bm{{X}}\right)^{-1}\bm{{\theta}}^{\mathbf{t}}\bm{{W}} + \left(\bm{{I}} - \rho \bm{{X}}\right)^{-1}\varepsilon

El siguiente fragmento de código simula un modelo SAR con un grafo de Bernoulli con 1,000 nodos y una densidad de 0.01. El proceso de generación de datos es el siguiente:

set.seed(4114)
n <- 1000

## Simulando la red
p <- 0.01
X <- matrix(rbinom(n^2, 1, p), nrow = n)

## Covariable
W <- matrix(rnorm(n), nrow = n)

## Simulando el resultado
rho <- 0.5
library(MASS) # Para la función mvrnorm

## Identidad menos rho * X
X_rowstoch <- X / rowSums(X)
I <- diag(n) - rho * X_rowstoch

## El resultado
Y <- solve(I) %*% (2 * W) + solve(I) %*% mvrnorm(1, rep(0, n), diag(n))

Usando el paquete de R spatialreg, podemos ajustar el modelo usando la función lagsarlm:

library(spdep) # para la función mat2listw
library(spatialreg)
fit <- lagsarlm(
  Y ~ W,
  data  = as.data.frame(X),
  listw = mat2listw(X_rowstoch)
  )

## Usando texreg para obtener una impresión bonita
texreg::screenreg(fit, single.row = TRUE)


========================================
                     Model 1            
----------------------------------------
(Intercept)             -0.01 (0.03)    
W                        1.97 (0.03) ***
rho                      0.54 (0.04) ***
----------------------------------------
Num. obs.             1000              
Parameters               4              
Log Likelihood       -1373.02           
AIC (Linear model)    2920.37           
AIC (Spatial model)   2754.05           
LR test: statistic     168.32           
LR test: p-value         0.00           
========================================
*** p < 0.001; ** p < 0.01; * p < 0.05

La interpretación de este modelo es casi la misma que una regresión lineal, con la diferencia de que tenemos el efecto de autocorrelación (rho). Como se esperaba, el modelo obtuvo una estimación lo suficientemente cercana al parámetro poblacional: \rho = 0.5.

Ejemplo de código: ALAAM

Hasta la fecha, no hay un paquete de R que implemente el marco ALAAM. Sin embargo, puedes ajustar ALAAMs usando el software PNet desarrollado por el grupo Melnet de la Universidad de Melbourne (haz clic aquí).

Debido a las similitudes, los ALAAMs pueden implementarse usando ERGMs. Debido a la novedad de esto, el ejemplo de código se dejará como un posible proyecto de clase. Publicaremos un ejemplo completo después del taller.

Coevolución

Finalmente, discutimos la coevolución cuando tanto la red como el comportamiento están embebidos en un bucle de retroalimentación. La coevolución debería ser la suposición predeterminada cuando se trata de redes sociales. Sin embargo, los modelos capaces de capturar la coevolución son difíciles de estimar. Aquí, discutiremos dos de tales modelos: Modelos Estocásticos Orientados al Actor (o Modelos Siena) (introducidos por primera vez en T. a. B. Snijders (1996); ver también T. A. B. Snijders (2017)) y Modelos de Red Exponencial Aleatorios de familia exponencial [ERNMs,] una generalización de ERGMs (Wang, Fellows, and Handcock 2023; Fellows 2012).

Siena Los Modelos Estocásticos Orientados al Actor [SOAMs] o Modelos Siena son modelos dinámicos de red y comportamiento que describen la transición de un sistema de red dentro de dos o más puntos de tiempo.

ERNMs Este modelo está estrechamente relacionado con los ERGMs, con la diferencia de que incorporan una salida a nivel de vértice. Conceptualmente, se está moviendo de tener una red aleatoria, a un modelo donde una característica de vértice dada y la red son aleatorias:

P_{\mathcal{Y}, \bm{{\theta}}}(\bm{{Y}}=\bm{{y}}|\bm{{X}}=\bm{{x}}) \to P_{\mathcal{Y}, \bm{{\theta}}}(\bm{{Y}}=\bm{{y}}, \bm{{X}}=\bm{{x}})

Ejemplo de código: Siena

Este ejemplo fue adaptado del paquete de R RSiena (ver página ?sienaGOF-auxiliary). Comenzamos cargando el paquete y echando un vistazo a los datos que usaremos:

library(RSiena)

## Visualizando la matriz de adyacencia y comportamiento
op <- par(mfrow=c(2, 2))
image(s501, main = "Red: s501")
image(s502, main = "Red: s502")
hist(s50a[,1], main = "Comp1")
hist(s50a[,2], main = "Comp2")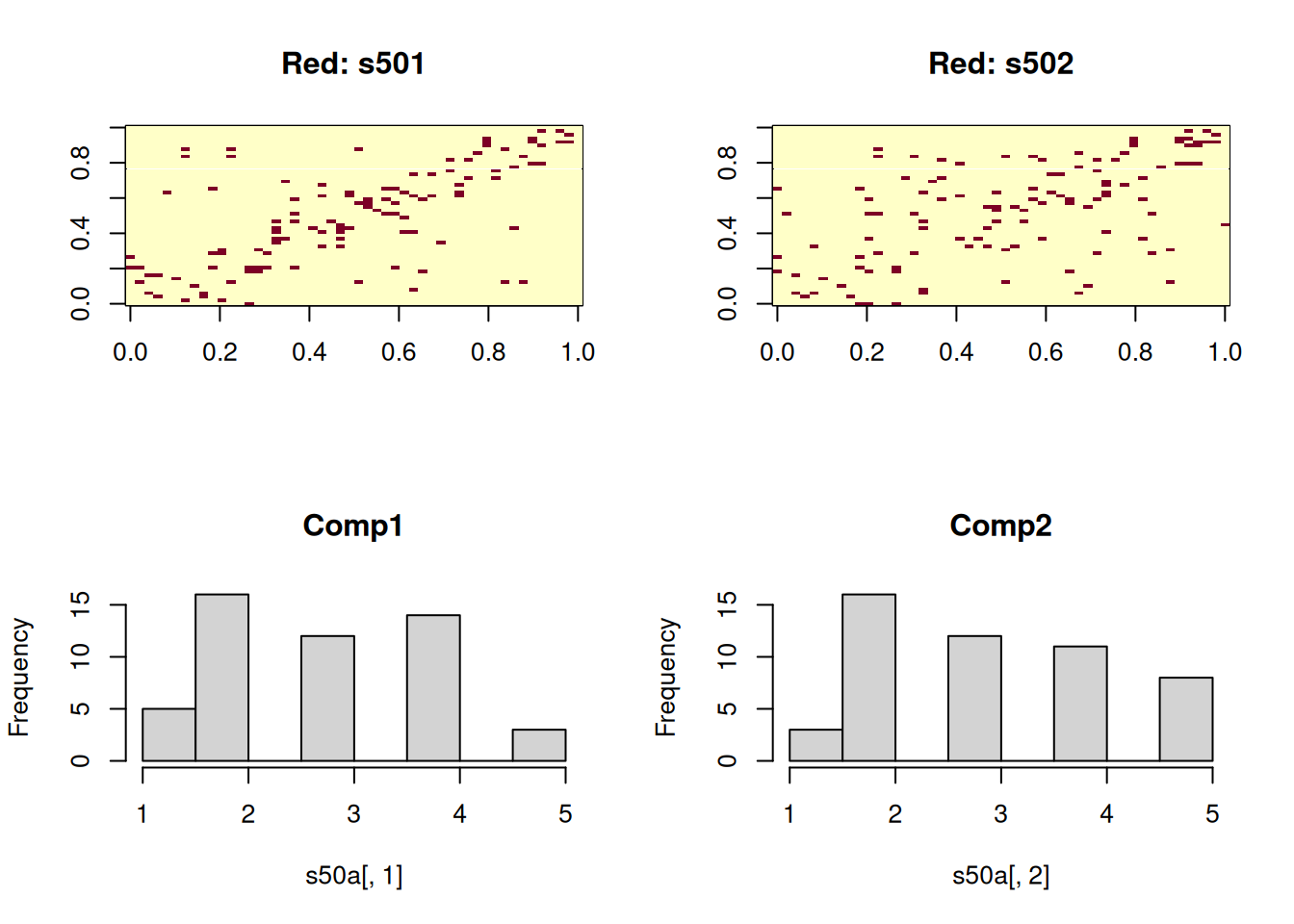

par(op)

El siguiente paso es el proceso de preparación de datos. RSiena no recibe datos crudos tal como están. Necesitamos declarar explícitamente las redes y la variable de resultado. Los modelos Siena también pueden modelar cambios de red

## Inicializando la variable dependiente (red)
mynet1 <- sienaDependent(array(c(s501, s502), dim=c(50, 50, 2)))
mynet1

Type         oneMode             
Observations 2                   
Nodeset      Actors (50 elements)

mybeh  <- sienaDependent(s50a[,1:2], type="behavior")
mybeh

Type         behavior            
Observations 2                   
Nodeset      Actors (50 elements)

## Covariables a nivel de nodo (artificiales)
mycov  <- c(rep(1:3,16),1,2)

## Covariables a nivel de enlace (también artificiales)
mydycov <- matrix(rep(1:5, 500), 50, 50)

## Creando el objeto de datos
mydata <- sienaDataCreate(mynet1, mybeh)

## Agregando los efectos (¡primero obtenerlos!)
myeff <- getEffects(mydata)

## Nota que Siena agrega algunos efectos predeterminados
myeff
##   name   effectName                  include fix   test  initialValue parm
## 1 mynet1 basic rate parameter mynet1 TRUE    FALSE FALSE    4.69604   0   
## 2 mynet1 outdegree (density)         TRUE    FALSE FALSE   -1.48852   0   
## 3 mynet1 reciprocity                 TRUE    FALSE FALSE    0.00000   0   
## 4 mybeh  rate mybeh period 1         TRUE    FALSE FALSE    0.70571   0   
## 5 mybeh  mybeh linear shape          TRUE    FALSE FALSE    0.32247   0   
## 6 mybeh  mybeh quadratic shape       TRUE    FALSE FALSE    0.00000   0

## Agregando algunos efectos extra (automáticamente los imprime)
myeff <- includeEffects(myeff, transTies, cycle3)
##   effectNumber effectName      shortName include fix   test  initialValue parm
## 1 41           3-cycles        cycle3    TRUE    FALSE FALSE          0   0   
## 2 44           transitive ties transTies TRUE    FALSE FALSE          0   0

Para agregar más efectos, primero, llama a la función effectsDocumentation(myeff). Te mostrará explícitamente cómo agregar un efecto particular. Por ejemplo, si quisiéramos agregar exposición de red (avExposure,) bajo la documentación de effectsDocumentation(myeff) necesitamos pasar los siguientes argumentos:

## Y ahora, efecto de exposición
myeff <- includeEffects(
  myeff,
  avExposure,
  # Estos últimos tres son especificados por effectsDocum...
  name         = "mybeh",
  interaction1 = "mynet1",
  type         = "rate"
  )

  effectNumber effectName                            shortName  include fix  
1 462          average exposure effect on rate mybeh avExposure TRUE    FALSE
  test  initialValue parm
1 FALSE          0   0

El siguiente paso involucra crear el modelo con (sienaAlgorithmCreate,) donde especificamos todos los parámetros para ajustar el modelo (ej., pasos MCMC.) Aquí, modificamos los valores de n3 y nsub a la mitad de los valores predeterminados para reducir el tiempo que tomaría ajustar el modelo; sin embargo esto degrada la calidad del ajuste.

## Fases 2 y 3 más cortas, solo para ejemplo:
myalgorithm <- sienaAlgorithmCreate(
  nsub = 2, n3 = 500, seed = 122, projname = NULL
  )
## If you use this algorithm object, siena07 will create/use an output file /tmp/RtmpJMZ4IJ/Siena1ab5a24779c.txt .
## This is a temporary file for this R session.
 
## Ajustando e imprimiendo el modelo
ans <- siena07(
  myalgorithm,
  data = mydata, effects = myeff,
  returnDeps = TRUE, batch = TRUE
  )
## 
## Start phase 0 
## theta:  4.696 -1.489  0.000  0.000  0.000  0.706  0.000  0.322  0.000 
## 
## Start phase 1 
## Phase 1 Iteration 1 Progress: 0%
## Phase 1 Iteration 2 Progress: 0%
## Phase 1 Iteration 3 Progress: 0%
## Phase 1 Iteration 4 Progress: 0%
## Phase 1 Iteration 5 Progress: 0%
## Phase 1 Iteration 10 Progress: 1%
## Phase 1 Iteration 15 Progress: 1%
## Phase 1 Iteration 20 Progress: 1%
## Phase 1 Iteration 25 Progress: 2%
## Phase 1 Iteration 30 Progress: 2%
## Phase 1 Iteration 35 Progress: 2%
## Phase 1 Iteration 40 Progress: 3%
## Phase 1 Iteration 45 Progress: 3%
## Phase 1 Iteration 50 Progress: 3%
## theta:  5.380 -1.734  0.481  0.147  0.166  1.168 -0.340  0.250  0.140 
## 
## Start phase 2.1
## Phase 2 Subphase 1 Iteration 1 Progress: 33%
## Phase 2 Subphase 1 Iteration 2 Progress: 33%
## theta  6.044 -1.877  0.840  0.300  0.473  1.096 -0.332  0.112  0.191 
## ac  0.375 -0.183  3.835  4.574 23.412  0.922  0.908  0.626  3.302 
## Phase 2 Subphase 1 Iteration 3 Progress: 33%
## Phase 2 Subphase 1 Iteration 4 Progress: 33%
## theta  6.1075 -2.0372  1.2512  0.0341  0.5207  1.2593 -0.1534  0.3018  0.1928 
## ac  0.9859  0.2280 -0.0703 -2.2973 -2.7455  1.1518  1.0749  0.8732  0.5399 
## Phase 2 Subphase 1 Iteration 5 Progress: 33%
## Phase 2 Subphase 1 Iteration 6 Progress: 33%
## theta  6.8650 -2.3185  1.7577  0.2694  0.7636  1.1997 -0.0433  0.3000  0.1762 
## ac  0.4789  0.4883  0.0199 -1.9449 -2.2609  1.1444  1.0397  0.9282  0.6470 
## Phase 2 Subphase 1 Iteration 7 Progress: 33%
## Phase 2 Subphase 1 Iteration 8 Progress: 33%
## theta  6.801140 -2.485273  1.966471  0.301197  0.817324  1.228010  0.000627  0.377719  0.072274 
## ac  0.4538  0.4933 -0.0158 -1.9326 -2.2588  1.1102  1.0395  0.9239  0.6905 
## Phase 2 Subphase 1 Iteration 9 Progress: 33%
## Phase 2 Subphase 1 Iteration 10 Progress: 33%
## theta  6.1258 -2.5124  1.8704  0.1206  0.6054  1.4538 -0.0145  0.5091 -0.0671 
## ac  0.472  0.103 -0.330 -1.625 -1.991  1.152  1.090  0.767  0.514 
## Phase 2 Subphase 1 Iteration 1 Progress: 33%
## Phase 2 Subphase 1 Iteration 2 Progress: 33%
## Phase 2 Subphase 1 Iteration 3 Progress: 33%
## Phase 2 Subphase 1 Iteration 4 Progress: 33%
## Phase 2 Subphase 1 Iteration 5 Progress: 33%
## Phase 2 Subphase 1 Iteration 6 Progress: 34%
## Phase 2 Subphase 1 Iteration 7 Progress: 34%
## Phase 2 Subphase 1 Iteration 8 Progress: 34%
## Phase 2 Subphase 1 Iteration 9 Progress: 34%
## Phase 2 Subphase 1 Iteration 10 Progress: 34%
## theta  6.4976 -2.5900  1.9265  0.2750  0.8543  1.0420  0.0446  0.3234 -0.0686 
## ac -0.212 -0.697 -0.818 -0.831 -0.765 -0.442 -0.268 -0.240 -0.267 
## theta:  6.4976 -2.5900  1.9265  0.2750  0.8543  1.0420  0.0446  0.3234 -0.0686 
## 
## Start phase 2.2
## Phase 2 Subphase 2 Iteration 1 Progress: 48%
## Phase 2 Subphase 2 Iteration 2 Progress: 48%
## Phase 2 Subphase 2 Iteration 3 Progress: 48%
## Phase 2 Subphase 2 Iteration 4 Progress: 48%
## Phase 2 Subphase 2 Iteration 5 Progress: 48%
## Phase 2 Subphase 2 Iteration 6 Progress: 48%
## Phase 2 Subphase 2 Iteration 7 Progress: 49%
## Phase 2 Subphase 2 Iteration 8 Progress: 49%
## Phase 2 Subphase 2 Iteration 9 Progress: 49%
## Phase 2 Subphase 2 Iteration 10 Progress: 49%
## theta  6.7988 -2.5810  1.9335  0.3941  0.7843  1.1111  0.0358  0.3252 -0.0415 
## ac -0.0757 -0.3672 -0.4025 -0.3676 -0.4157 -0.0166  0.0222 -0.0874  0.0651 
## theta:  6.7988 -2.5810  1.9335  0.3941  0.7843  1.1111  0.0358  0.3252 -0.0415 
## 
## Start phase 3 
## Phase 3 Iteration 500 Progress 100%

ans
## Estimates, standard errors and convergence t-ratios
## 
##                                                 Estimate   Standard   Convergence 
##                                                              Error      t-ratio   
## Network Dynamics 
##   1. rate basic rate parameter mynet1            6.7988  ( 1.2496   )   -0.0460   
##   2. eval outdegree (density)                   -2.5810  ( 0.1505   )    0.0113   
##   3. eval reciprocity                            1.9335  ( 0.2627   )    0.0205   
##   4. eval 3-cycles                               0.3941  ( 0.2742   )   -0.0658   
##   5. eval transitive ties                        0.7843  ( 0.2379   )   -0.0014   
## 
## Behavior Dynamics
##   6. rate rate mybeh period 1                    1.1111  ( 1.3096   )   -0.0199   
##   7. rate average exposure effect on rate mybeh  0.0358  ( 0.4373   )   -0.0190   
##   8. eval mybeh linear shape                     0.3252  ( 0.2329   )   -0.0048   
##   9. eval mybeh quadratic shape                 -0.0415  ( 0.1139   )    0.0992   
## 
## Overall maximum convergence ratio:    0.2163 
## 
## 
## Total of 940 iteration steps.

Como regla general, valores t absolutos por debajo de 0.1 muestran buena convergencia, por debajo de 0.2 decimos “razonablemente bien,” y por encima no hay convergencia. Resaltemos dos de los efectos que tenemos en nuestro modelo

Los vínculos transitivos (número cinco) son positivos 0.78 con un valor t menor que 0.01. Por lo tanto, decimos que la red tiene una tendencia hacia la transitividad (equilibrio) que es significativa.
El efecto de exposición (número siete) también es positivo, pero pequeño, 0.03, pero aún significativo (valor t de -0.01)

Como con ERGMs, también hacemos bondad de ajuste:

sienaGOF(ans, OutdegreeDistribution, varName="mynet1") |>
  plot()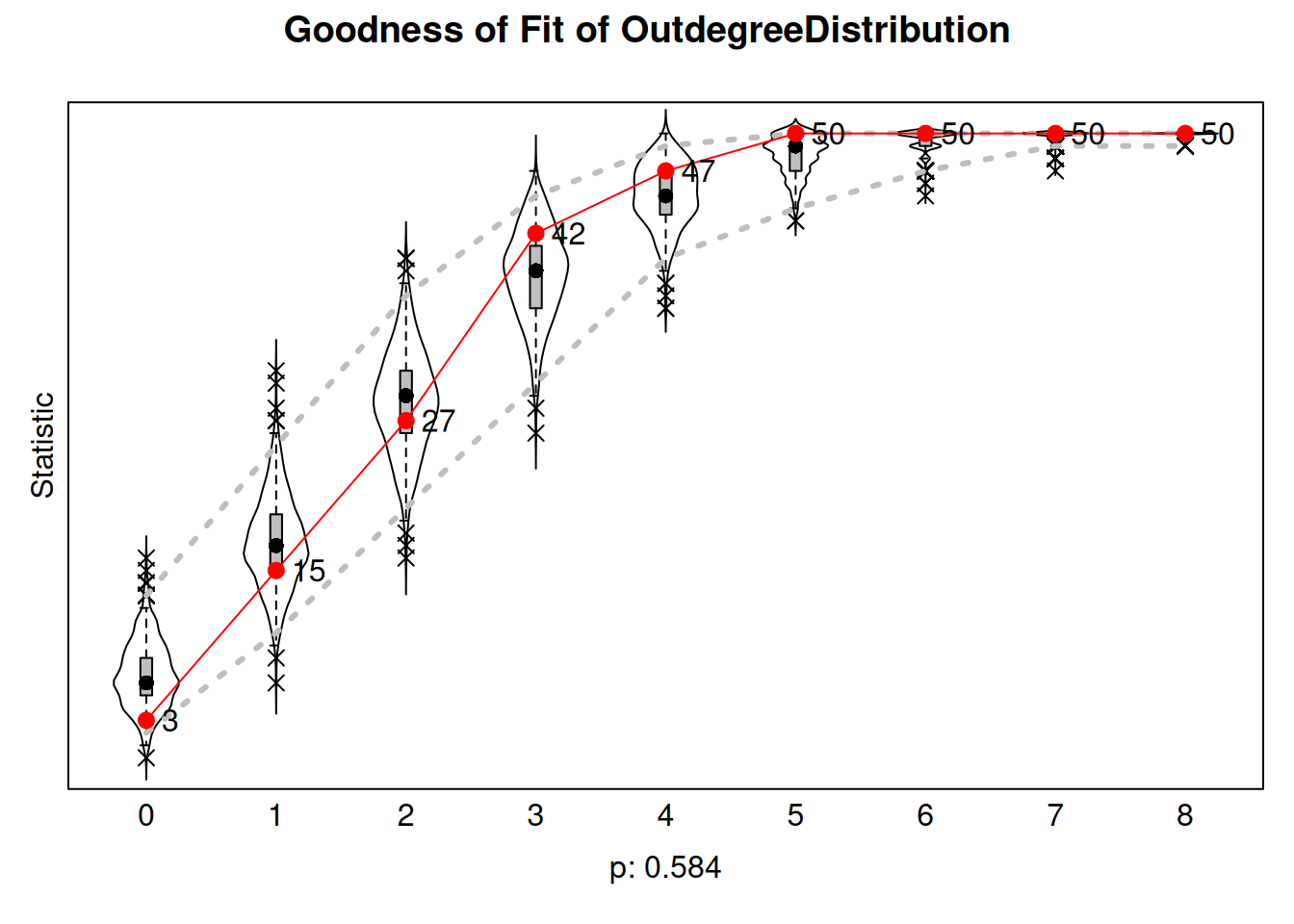

sienaGOF(ans, BehaviorDistribution, varName = "mybeh") |> 
  plot()

Note: some statistics are not plotted because their variance is 0.
This holds for the statistic: 5.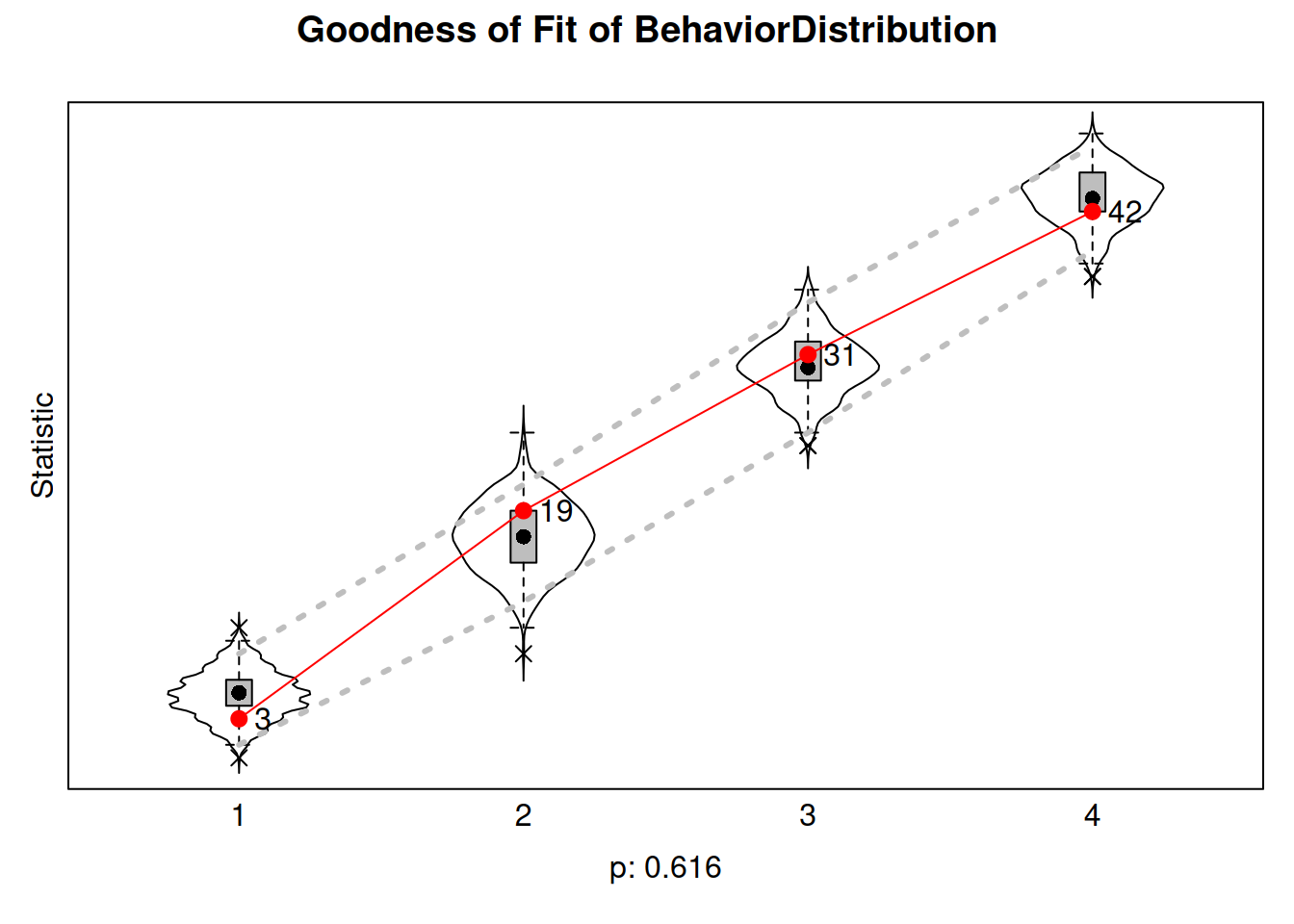

Ejemplo de código: ERNM

Hasta la fecha, no hay un lanzamiento CRAN para el modelo ERNM. La única implementación de la que estoy al tanto es de uno de los autores principales, que está disponible en GitHub: https://github.com/fellstat/ernm. Desafortunadamente, la versión actual del paquete parece estar rota.

Al igual que el caso ALAAM, como los ERNMs están estrechamente relacionados con los ERGMS, ¡construir un ejemplo usando el paquete ERGM podría ser una gran oportunidad para un proyecto de clase!

Fellows, Ian E. 2012. “Exponential Family Random Network Models.” ProQuest Dissertations and Theses. PhD thesis. https://login.ezproxy.lib.utah.edu/login?url=https://www.proquest.com/dissertations-theses/exponential-family-random-network-models/docview/1221548720/se-2.

Handcock, Mark S., David R. Hunter, Carter T. Butts, Steven M. Goodreau, Pavel N. Krivitsky, and Martina Morris. 2023. Ergm: Fit, Simulate and Diagnose Exponential-Family Models for Networks. The Statnet Project (https://statnet.org). https://CRAN.R-project.org/package=ergm.

Haye, Kayla de la, Heesung Shin, George G. Vega Yon, and Thomas W. Valente. 2019. “Smoking Diffusion Through Networks of Diverse, Urban American Adolescents over the High School Period.” Journal of Health and Social Behavior. https://doi.org/10.1177/0022146519870521.

Hunter, David R., Mark S. Handcock, Carter T. Butts, Steven M. Goodreau, and Martina Morris. 2008. “ergm : A Package to Fit, Simulate and Diagnose Exponential-Family Models for Networks.” Journal of Statistical Software 24 (3). https://doi.org/10.18637/jss.v024.i03.

LeSage, James P. 2008. “An Introduction to Spatial Econometrics.” Revue d’économie Industrielle 123 (123): 19–44. https://doi.org/10.4000/rei.3887.

LeSage, James P., and R. Kelley Pace. 2014. “The Biggest Myth in Spatial Econometrics.” Econometrics 2 (4): 217–49. https://doi.org/10.2139/ssrn.1725503.

Robins, Garry, Philippa Pattison, and Peter Elliott. 2001. “Network Models for Social Influence Processes.” Psychometrika 66 (2): 161–89. https://doi.org/10.1007/BF02294834.

Roger Bivand. 2022. “R Packages for Analyzing Spatial Data: A Comparative Case Study with Areal Data.” Geographical Analysis 54 (3): 488–518. https://doi.org/10.1111/gean.12319.

Snijders, Tom a B. 1996. “Stochastic Actor-Oriented Models for Network Change.” The Journal of Mathematical Sociology 21 (1-2): 149–72. https://doi.org/10.1080/0022250X.1996.9990178.

Snijders, Tom A. B. 2017. “Stochastic Actor-Oriented Models for Network Dynamics.” Annual Review of Statistics and Its Application 4 (1): 343–63. https://doi.org/10.1146/annurev-statistics-060116-054035.

Valente, Thomas W., and George G. Vega Yon. 2020. “Diffusion/Contagion Processes on Social Networks.” Health Education & Behavior 47 (2): 235–48. https://doi.org/10.1177/1090198120901497.

Valente, Thomas W., Heather Wipfli, and George G. Vega Yon. 2019. “Network Influences on Policy Implementation: Evidence from a Global Health Treaty.” Social Science and Medicine. https://doi.org/10.1016/j.socscimed.2019.01.008.

Wang, Zeyi, Ian E. Fellows, and Mark S. Handcock. 2023. “Understanding Networks with Exponential-Family Random Network Models.” Social Networks, August, S0378873323000497. https://doi.org/10.1016/j.socnet.2023.07.003.