Exponential Random Graph Models

Published

June 27, 2024

Modified

September 3, 2025

I strongly suggest reading the vignette in the ergm R package.

vignette("ergm", package="ergm")

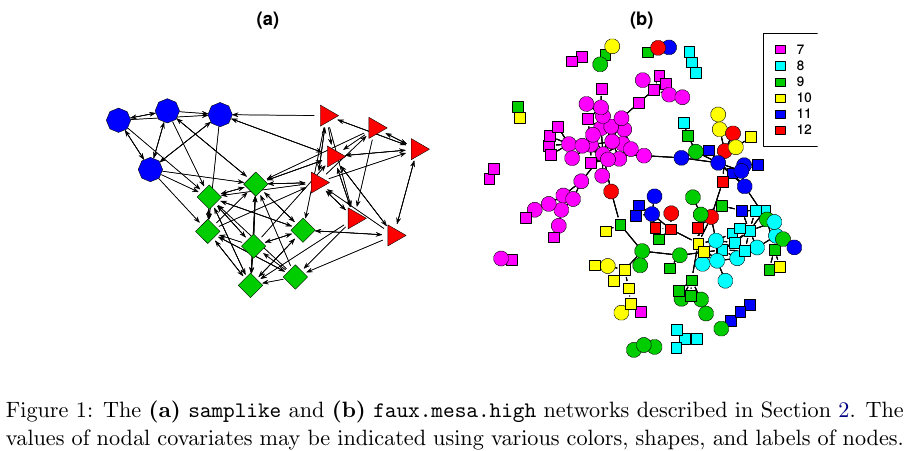
The purpose of ERGMs, in a nutshell, is to describe parsimoniously the local selection forces that shape the global structure of a network. To this end, a network dataset, like those depicted in Figure 1, may be considered as the response in a regression model, where the predictors are things like “propensity for individuals of the same sex to form partnerships” or “propensity for individuals to form triangles of partnerships”. In Figure 1(b), for example, it is evident that the individual nodes appear to cluster in groups of the same numerical labels (which turn out to be students’ grades, 7 through 12); thus, an ERGM can help us quantify the strength of this intra-group effect.

— (David R. Hunter et al. 2008)

Source: Hunter et al. (2008)

In a nutshell, we use ERGMs as a parametric interpretation of the distribution of \mathbf{Y}, which takes the canonical form:

{\mathbb{P}_{\mathcal{Y}}\left(\mathbf{Y}=\mathbf{y};\mathbf{\theta}\right) } = \frac{\text{exp}\left\{\theta^{\text{T}}\mathbf{g}(\mathbf{y})\right\}}{\kappa\left(\theta, \mathcal{Y}\right)},\quad\mathbf{y}\in\mathcal{Y} \tag{9.1}

Where \theta\in\Omega\subset\mathbb{R}^q is the vector of model coefficients and \mathbf{g}(\mathbf{y}) is a q-vector of statistics based on the adjacency matrix \mathbf{y}.

Model Equation 9.1 may be expanded by replacing \mathbf{g}(\mathbf{y}) with \mathbf{g}(\mathbf{y}, \mathbf{X}) to allow for additional covariate information \mathbf{X} about the network. The denominator \kappa\left(\theta,\mathcal{Y}\right) = \sum_{\mathbf{y}\in\mathcal{Y}}\text{exp}\left\{\theta^{\text{T}}\mathbf{g}(\mathbf{y})\right\} is the normalizing factor that ensures that equation Equation 9.1 is a legitimate probability distribution. Even after fixing \mathcal{Y} to be all the networks that have size n, the size of \mathcal{Y} makes this type of statistical model hard to estimate as there are N = 2^{n(n-1)} possible networks! (David R. Hunter et al. 2008)

Later developments include new dependency structures to consider more general neighborhood effects. These models relax the one-step Markovian dependence assumptions, allowing investigation of longer-range configurations, such as longer paths in the network or larger cycles (Pattison and Robins 2002). Models for bipartite (Faust and Skvoretz 1999) and tripartite (Mische and Robins 2000) network structures have been developed. (David R. Hunter et al. 2008, 9)

A naïve example

In the simplest case, ERGMs equate a logistic regression. By simple, I mean cases with no Markovian terms–motifs involving more than one edge–for example, the Bernoulli graph. In the Bernoulli graph, ties are independent, so the presence/absence of a tie between nodes i and j won’t affect the presence/absence of a tie between nodes k and l.

Let’s fit an ERGM using the sampson dataset in the ergm package.

library(ergm)
library(netplot)
data("sampson")
nplot(samplike)

Using ergm to fit a Bernoulli graph requires using the edges term, which counts how many ties are in the graph:

ergm_fit <- ergm(samplike ~ edges)
## Starting maximum pseudolikelihood estimation (MPLE):
## Obtaining the responsible dyads.
## Evaluating the predictor and response matrix.
## Maximizing the pseudolikelihood.
## Finished MPLE.
## Evaluating log-likelihood at the estimate.

Since this is equivalent to a logistic regression, we can use the glm function to fit the same model. First, we need to prepare the data so we can pass it to glm:

y <- sort(as.vector(as.matrix(samplike)))
y <- y[-c(1:18)] # We remove the diagonal from the model, which is all 0.
y
##   [1] 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
##  [38] 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
##  [75] 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
## [112] 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
## [149] 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
## [186] 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1
## [223] 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
## [260] 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
## [297] 1 1 1 1 1 1 1 1 1 1

We can now fit the GLM model:

glm_fit <- glm(y~1, family=binomial("logit"))

The coefficients of both ERGM and GLM should match:

glm_fit
## 
## Call:  glm(formula = y ~ 1, family = binomial("logit"))
## 
## Coefficients:
## (Intercept)  
##     -0.9072  
## 
## Degrees of Freedom: 305 Total (i.e. Null);  305 Residual
## Null Deviance:       367.2 
## Residual Deviance: 367.2     AIC: 369.2
ergm_fit
## 
## Call:
## ergm(formula = samplike ~ edges)
## 
## Maximum Likelihood Coefficients:
##   edges  
## -0.9072

Furthermore, in the case of the Bernoulli graph, we can get the estimate using the Logit function:

pr <- mean(y)
# Logit function:
# Alternatively we could have used log(pr) - log(1-pr)
qlogis(pr)
## [1] -0.9071582

Again, the same result. The Bernoulli graph is not the only ERGM model that can be fitted using a Logistic regression. Moreover, if all the terms of the model are non-Markov terms, ergm automatically defaults to a Logistic regression.

Estimation of ERGMs

The ultimate goal is to perform statistical inference on the proposed model. In a standard setting, we could use Maximum Likelihood Estimation (MLE), which consists of finding the model parameters \theta that, given the observed data, maximize the likelihood of the model. For the latter, we generally use Newton’s method. Newton’s method requires computing the model’s log-likelihood, which can be challenging in ERGMs.

For ERGMs, since part of the likelihood involves a normalizing constant that is a function of all possible networks, this is not as straightforward as in the regular setting. Because of this, most estimation methods rely on simulations.

In statnet, the default estimation method is based on a method proposed by (Geyer and Thompson 1992), Markov-Chain MLE, which uses Markov-Chain Monte Carlo for simulating networks and a modified version of the Newton-Raphson algorithm to estimate the parameters.

The idea of MC-MLE for this family of statistical models is to approximate the expectation of normalizing constant ratios using the law of large numbers. In particular, the following:

\begin{align*} \frac{\kappa\left(\theta,\mathcal{Y}\right)}{\kappa\left(\theta_0,\mathcal{Y}\right)} & = \frac{ \sum_{\mathbf{y}\in\mathcal{Y}}\text{exp}\left\{\theta^{\text{T}}\mathbf{g}(\mathbf{y})\right\}}{ \sum_{\mathbf{y}\in\mathcal{Y}}\text{exp}\left\{\theta_0^{\text{T}}\mathbf{g}(\mathbf{y})\right\} } \\ & = \sum_{\mathbf{y}\in\mathcal{Y}}\left( % \frac{1}{% \sum_{\mathbf{y}\in\mathcal{Y}\text{exp}\left\{\theta_0^{\text{T}}\mathbf{g}(\mathbf{y})\right\}}% } \times % \text{exp}\left\{\theta^{\text{T}}\mathbf{g}(\mathbf{y})\right\} % \right) \\ & = \sum_{\mathbf{y}\in\mathcal{Y}}\left( % \frac{\text{exp}\left\{\theta_0^{\text{T}}\mathbf{g}(\mathbf{y})\right\}}{% \sum_{\mathbf{y}\in\mathcal{Y}\text{exp}\left\{\theta_0^{\text{T}}\mathbf{g}(\mathbf{y})\right\}}% } \times % \text{exp}\left\{(\theta - \theta_0)^{\text{T}}\mathbf{g}(\mathbf{y})\right\} % \right) \\ & = \sum_{\mathbf{y}\in\mathcal{Y}}\left( % {\mathbb{P}_{\times }\left(Y = y|\mathcal{Y}, \theta_0\right) }% \text{exp}\left\{(\theta - \theta_0)^{\text{T}}\mathbf{g}(\mathbf{y})\right\} % \right) \\ & = \text{E}_{\theta_0}\left(\text{exp}\left\{(\theta - \theta_0)^{\text{T}}\mathbf{g}(\mathbf{y})\right\} \right) \end{align*}

In particular, the MC-MLE algorithm uses this fact to maximize the log-likelihood ratio. The objective function itself can be approximated by simulating m networks from the distribution with parameter \theta_0:

l(\theta) - l(\theta_0) \approx (\theta - \theta_0)^{\text{T}}\mathbf{g}(\mathbf{y}_{obs}) - \text{log}{\left[\frac{1}{m}\sum_{i = 1}^m\text{exp}\left\{(\theta-\theta_0)^{\text{T}}\right\}\mathbf{g}(\mathbf{Y}_i)\right]}

For more details, see (David R. Hunter et al. 2008). A sketch of the algorithm follows:

  1. Initialize the algorithm with an initial guess of \theta, call it \theta^{(t)} (must be a rather OK guess)

  2. While (no convergence) do:

  1. Using \theta^{(t)}, simulate M networks by means of small changes in the \mathbf{Y}_{obs} (the observed network). This part is done by using an importance-sampling method which weights each proposed network by its likelihood conditional on \theta^{(t)}

  2. With the networks simulated, we can do the Newton step to update the parameter \theta^{(t)} (this is the iteration part in the ergm package): \theta^{(t)}\to\theta^{(t+1)}.

  3. If convergence has been reached (which usually means that \theta^{(t)} and \theta^{(t + 1)} are not very different), then stop; otherwise, go to step a.

Lusher, Koskinen, and Robins (2013);Admiraal and Handcock (2006);Snijders (2002);Wang et al. (2009) provides details on the algorithm used by PNet (the same as the one used in RSiena), and Lusher, Koskinen, and Robins (2013) provides a short discussion on the differences between ergm and PNet.

The ergm package

From the previous section:1

library(igraph)

library(dplyr)

load("03.rda")

In this section, we will use the ergm package (from the statnet suit of packages Handcock et al. (2023),) and the intergraph (Bojanowski 2023) package. The latter provides functions to go back and forth between igraph and network objects from the igraph and network packages respectively2

library(ergm)
library(intergraph)

As a rather important side note, the order in which R packages are loaded matters. Why is this important to mention now? Well, it turns out that at least a couple of functions in the network package have the same name as some functions in the igraph package. When the ergm package is loaded, since it depends on network, it will load the network package first, which will mask some functions in igraph. This becomes evident once you load ergm after loading igraph:

The following objects are masked from ‘package:igraph’:

  add.edges, add.vertices, %c%, delete.edges, delete.vertices, get.edge.attribute, get.edges,
  get.vertex.attribute, is.bipartite, is.directed, list.edge.attributes, list.vertex.attributes, %s%,
  set.edge.attribute, set.vertex.attribute

What are the implications of this? If you call the function list.edge.attributes for an object of class igraph R will return an error as the first function that matches that name comes from the network package! To avoid this you can use the double colon notation:

igraph::list.edge.attributes(my_igraph_object)
network::list.edge.attributes(my_network_object)

Using the asNetwork function, we can coerce the igraph object into a network object so we can use it with the ergm function:

# Creating the new network
network_111 <- intergraph::asNetwork(ig_year1_111)

# Running a simple ergm (only fitting edge count)
ergm(network_111 ~ edges)
## Warning in ergm.getnetwork(formula): This network contains loops
## Starting maximum pseudolikelihood estimation (MPLE):
## Obtaining the responsible dyads.
## Evaluating the predictor and response matrix.
## Maximizing the pseudolikelihood.
## Finished MPLE.
## Evaluating log-likelihood at the estimate.
## 
## Call:
## ergm(formula = network_111 ~ edges)
## 
## Maximum Likelihood Coefficients:
##  edges  
## -4.734

So what happened here? We got a warning. It turns out that our network has loops (didn’t think about it before!). Let’s take a look at that with the which_loop function

E(ig_year1_111)[which_loop(ig_year1_111)]
## + 1/2638 edge from e008b94 (vertex names):
## [1] 1110111->1110111

We can get rid of these using the igraph::-.igraph. Let’s remove the isolates using the same operator

# Creating the new network
network_111 <- ig_year1_111

# Removing loops
network_111 <- network_111 - E(network_111)[which(which_loop(network_111))]

# Removing isolates
network_111 <- network_111 - which(degree(network_111, mode = "all") == 0)

# Converting the network
network_111 <- intergraph::asNetwork(network_111)

asNetwork(simplify(ig_year1_111)) ig_year1_111 |> simplify() |> asNetwork()

A problem that we have with this data is the fact that some vertices have missing values in the variables hispanic, female1, and eversmk1. For now, we will proceed by imputing values based on the averages:

for (v in c("hispanic", "female1", "eversmk1")) {
  tmpv <- network_111 %v% v
  tmpv[is.na(tmpv)] <- mean(tmpv, na.rm = TRUE) > .5
  network_111 %v% v <- tmpv
}

Let’s take a look at the network

nplot(
  network_111,
  vertex.color = ~ hispanic
  )
Figure 9.1

Coloring by hispanic, we can see that nodes seem to be clustered by this attribute. Visual inspection in network science can be very useful, but, in order to make more formal statements, we need to use statistical models; this is where ERGMs shine.

Estimating ERGMs

Although there is no silver bullet for estimating these models, the following workflow has worked for me in the past:

  1. Estimate the simplest model, adding one variable at a time.

  2. After each estimation, run the mcmc.diagnostics function to see how good (or bad) behaved the chains are.

  3. Run the gof function and verify how good the model matches the network’s structural statistics.

What to use:

  1. control.ergms: Maximum number of iterations, seed for Pseudo-RNG, how many cores

  2. ergm.constraints: Where to sample the network from. Gives stability and (in some cases) faster convergence as by constraining the model you are reducing the sample size.

Here is an example of a couple of models that we could compare

Note

Notice that this document may not include the usual messages that the ergm command generates during the estimation procedure. This is just to make it more printable-friendly.

ans0 <- ergm(
  network_111 ~
    edges +
    nodematch("hispanic") +
    nodematch("female1") +
    nodematch("eversmk1") +
    mutual,
  control = control.ergm(
    seed        = 1,
    MCMLE.maxit = 10,
    parallel    = 4,
    CD.maxit    = 10
    )
  )
## Warning: 'glpk' selected as the solver, but package 'Rglpk' is not available;
## falling back to 'lpSolveAPI'. This should be fine unless the sample size and/or
## the number of parameters is very big.
Previous version of the book

In a previous version of the book we used the bd constraint to limit the maximum number of outgoing ties to 19. Although this is a reasonable constraint (as the sample may have been restricted by construction), the current version of the ERGM package returns a warning and shows the GOF statistics with switched signs (negative AIC and BIC, and positive Loglikelihood).

So what are we doing here:

  1. The model is controlling for:

    1. edges Number of edges in the network (as opposed to its density)

    2. nodematch("some-variable-name-here") Includes a term that controls for homophily/heterophily

    3. mutual Number of mutual connections between (i, j), (j, i). This can be related to, for example, triadic closure.

For more on control parameters, see Morris, Handcock, and Hunter (2008). The next model consists of a simpler version. Excluding the mutual term leads to an ERGM with no Markov terms, meaning that all the sufficient statistics are functions of individual edges rather than configurations involving multiple edges. The mutual term, by contrast, involves pairs of ties (i \to j and j \to i), which is an example of a Markov term. Models with only non-Markov terms reduce to a logistic regression, which is why the fitting process avoids using MCMC:

ans1 <- ergm(
  network_111 ~
    edges +
    nodematch("hispanic") +
    nodematch("female1") +
    nodematch("eversmk1")
    ,
  control = control.ergm(
    seed        = 1,
    MCMLE.maxit = 10,
    parallel    = 4,
    CD.maxit    = 10
    )
  )

Finally, we can try incorporating a more complex term, for example, the geometrically weighted edge-wise shared partners (gwesp) term. This term is akin to triadic closure, but it is easier to estimate. Moreover, to ease the estimation process, it is recommended to add the geometrically weighted dyad-wise shared partners (gwdsp) term too. Both terms include a decay parameter; for simplicity, both will be fixed and set to be 0.5 (values between 0.25 and 1.5 are common). For more on this, see David R. Hunter (2007).

ans2 <- ergm(
  network_111 ~
    edges +
    nodematch("hispanic") +
    nodematch("female1") +
    nodematch("eversmk1") + 
    mutual +
    gwesp(decay = 0.5, fixed = TRUE) +
    gwdsp(decay = 0.5, fixed = TRUE)
    ,
  control = control.ergm(
    seed        = 1,
    MCMLE.maxit = 10,
    parallel    = 4,
    CD.maxit    = 10
    )
  )

Now, a nice trick to see all regressions in the same table, we can use the texreg package (Leifeld 2013) which supports ergm ouputs!

library(texreg)
## Version:  1.39.4
## Date:     2024-07-23
## Author:   Philip Leifeld (University of Manchester)
## 
## Consider submitting praise using the praise or praise_interactive functions.
## Please cite the JSS article in your publications -- see citation("texreg").
screenreg(list(ans0, ans1, ans2))
## 
## ================================================================
##                      Model 1        Model 2        Model 3      
## ----------------------------------------------------------------
## edges                    -5.62 ***      -5.49 ***      -4.73 ***
##                          (0.05)         (0.06)         (0.07)   
## nodematch.hispanic        0.22 ***       0.30 ***       0.16 ***
##                          (0.04)         (0.05)         (0.03)   
## nodematch.female1         0.87 ***       1.16 ***       0.47 ***
##                          (0.04)         (0.05)         (0.03)   
## nodematch.eversmk1        0.33 ***       0.45 ***       0.23 ***
##                          (0.04)         (0.04)         (0.03)   
## mutual                    4.10 ***                      2.72 ***
##                          (0.07)                        (0.08)   
## gwesp.OTP.fixed.0.5                                     1.34 ***
##                                                        (0.03)   
## gwdsp.OTP.fixed.0.5                                    -0.11 ***
##                                                        (0.01)   
## ----------------------------------------------------------------
## AIC                   22649.55       25135.63       20155.83    
## BIC                   22699.89       25175.91       20226.31    
## Log Likelihood       -11319.77      -12563.82      -10070.91    
## ================================================================
## *** p < 0.001; ** p < 0.01; * p < 0.05

Or, if you are using rmarkdown, you can export the results using LaTeX or html, let’s try the latter to see how it looks like here:

library(texreg)
htmlreg(list(ans0, ans1, ans2))
Statistical models
  Model 1 Model 2 Model 3
edges -5.62*** -5.49*** -4.73***
  (0.05) (0.06) (0.07)
nodematch.hispanic 0.22*** 0.30*** 0.16***
  (0.04) (0.05) (0.03)
nodematch.female1 0.87*** 1.16*** 0.47***
  (0.04) (0.05) (0.03)
nodematch.eversmk1 0.33*** 0.45*** 0.23***
  (0.04) (0.04) (0.03)
mutual 4.10***   2.72***
  (0.07)   (0.08)
gwesp.OTP.fixed.0.5     1.34***
      (0.03)
gwdsp.OTP.fixed.0.5     -0.11***
      (0.01)
AIC 22649.55 25135.63 20155.83
BIC 22699.89 25175.91 20226.31
Log Likelihood -11319.77 -12563.82 -10070.91
***p < 0.001; **p < 0.01; *p < 0.05

Before we go to the next section, let’s make some comments on what we see in the table:

  1. Of the three models, the last one is the best in terms of smallest AIC and BIC, and largest Loglikelihood.

  2. All the nodematch terms are significant and positive, which means that we have homophily by hispanic, female1, and eversmk1.

  3. The mutual term is significant, positive, and large (~4). This indicates a strong tendency for individuals to befriend each other.

  4. The gwesp term is positive and significant. The interpretation of this term is not always simple. Generally, we say that a positive gwesp term means that there is a tendency for triadic closure.

Model Goodness-of-Fit

In raw terms, once each chain has reached stationary distribution, we can say that there are no problems with autocorrelation and that each sample point is iid. The latter implies that, since we are running the model with more than one chain, we can use all the samples (chains) as a single dataset.

Recent changes in the ergm estimation algorithm mean that these plots can no longer be used to ensure that the mean statistics from the model match the observed network statistics. For that functionality, please use the GOF command: gof(object, GOF=~model).

—?ergm::mcmc.diagnostics

Since ans2 is the best model, let’s look at the GOF statistics. First, let’s see how the MCMC did. We can use the mcmc.diagnostics function included in the package. The function is a wrapper of a couple of functions from the coda package (Plummer et al. 2006), which are called upon the $sample object holding the centered statistics from the sampled networks. At first, it can be confusing to look at the $sample object; it neither matches the observed statistics nor the coefficients.

When calling mcmc.diagnostics(ans2, centered = FALSE), you will see many outputs, including a couple of plots showing the trace and posterior distribution of the uncentered statistics (centered = FALSE). The following code chunks will reproduce the output from the mcmc.diagnostics function step by step using the coda package. First, we need to uncenter the sample object:

# Getting the centered sample
sample_centered <- ans2$sample

# Getting the observed statistics and turning it into a matrix so we can add it
# to the samples
observed <- summary(ans2$formula)
observed <- matrix(
  observed,
  nrow  = nrow(sample_centered[[1]]),
  ncol  = length(observed),
  byrow = TRUE
  )

# Now we uncenter the sample
sample_uncentered <- lapply(sample_centered, function(x) {
  x + observed
})

# We have to make it an mcmc.list object
sample_uncentered <- coda::mcmc.list(sample_uncentered)

Under the hood:

  1. Empirical means and sd, and quantiles:
summary(sample_uncentered)
## 
## Iterations = 327680:5963776
## Thinning interval = 32768 
## Number of chains = 4 
## Sample size per chain = 173 
## 
## 1. Empirical mean and standard deviation for each variable,
##    plus standard error of the mean:
## 
##                        Mean     SD Naive SE Time-series SE
## edges                2471.9  63.94    2.430          6.221
## nodematch.hispanic   1829.8  59.02    2.244          7.099
## nodematch.female1    1874.4  71.09    2.703          8.346
## nodematch.eversmk1   1755.6  58.02    2.206          6.746
## mutual                481.9  27.72    1.054          3.379
## gwesp.OTP.fixed.0.5  1762.6 113.98    4.333         13.574
## gwdsp.OTP.fixed.0.5 13175.1 644.91   24.516         66.387
## 
## 2. Quantiles for each variable:
## 
##                        2.5%   25%   50%   75% 97.5%
## edges                2347.3  2431  2469  2510  2605
## nodematch.hispanic   1718.3  1791  1827  1867  1955
## nodematch.female1    1736.0  1827  1871  1928  2016
## nodematch.eversmk1   1654.3  1714  1752  1794  1879
## mutual                429.3   462   481   500   542
## gwesp.OTP.fixed.0.5  1540.9  1684  1760  1835  2013
## gwdsp.OTP.fixed.0.5 11958.3 12737 13137 13596 14488
  1. Cross correlation:
coda::crosscorr(sample_uncentered)
##                         edges nodematch.hispanic nodematch.female1
## edges               1.0000000          0.8566830         0.8770210
## nodematch.hispanic  0.8566830          1.0000000         0.7573169
## nodematch.female1   0.8770210          0.7573169         1.0000000
## nodematch.eversmk1  0.8229030          0.6949758         0.7455362
## mutual              0.7921269          0.7019044         0.7765035
## gwesp.OTP.fixed.0.5 0.8782943          0.7780147         0.8679069
## gwdsp.OTP.fixed.0.5 0.9678268          0.8370254         0.8591945
##                     nodematch.eversmk1    mutual gwesp.OTP.fixed.0.5
## edges                        0.8229030 0.7921269           0.8782943
## nodematch.hispanic           0.6949758 0.7019044           0.7780147
## nodematch.female1            0.7455362 0.7765035           0.8679069
## nodematch.eversmk1           1.0000000 0.7067807           0.7820246
## mutual                       0.7067807 1.0000000           0.8954091
## gwesp.OTP.fixed.0.5          0.7820246 0.8954091           1.0000000
## gwdsp.OTP.fixed.0.5          0.8098323 0.7688635           0.8575789
##                     gwdsp.OTP.fixed.0.5
## edges                         0.9678268
## nodematch.hispanic            0.8370254
## nodematch.female1             0.8591945
## nodematch.eversmk1            0.8098323
## mutual                        0.7688635
## gwesp.OTP.fixed.0.5           0.8575789
## gwdsp.OTP.fixed.0.5           1.0000000
  1. Autocorrelation_: For now, we will only look at autocorrelation for chain one. Autocorrelation should be small (in a general MCMC setting). If autocorrelation is high, then it means that your sample is not idd (no Markov property). A way to solve this is thinning the sample.
coda::autocorr(sample_uncentered)[[1]]
## , , edges
## 
##                   edges nodematch.hispanic nodematch.female1 nodematch.eversmk1
## Lag 0       1.000000000         0.85174677        0.90035143         0.84731435
## Lag 32768   0.604509897         0.52958876        0.66467595         0.54146395
## Lag 163840  0.369212891         0.35412936        0.40011462         0.39283115
## Lag 327680  0.184463035         0.14706318        0.24305479         0.29114538
## Lag 1638400 0.009007472        -0.02631294        0.03456016        -0.04578478
##                 mutual gwesp.OTP.fixed.0.5 gwdsp.OTP.fixed.0.5
## Lag 0       0.83296982           0.9136663          0.97089215
## Lag 32768   0.68928494           0.6870541          0.57938173
## Lag 163840  0.45203629           0.4511364          0.36536136
## Lag 327680  0.12747154           0.1829741          0.15036241
## Lag 1638400 0.05607638           0.0292786         -0.01022981
## 
## , , nodematch.hispanic
## 
##                   edges nodematch.hispanic nodematch.female1 nodematch.eversmk1
## Lag 0       0.851746774         1.00000000       0.796948280         0.77244980
## Lag 32768   0.540210932         0.64168452       0.620791472         0.51899205
## Lag 163840  0.348421398         0.40142712       0.409478507         0.40705581
## Lag 327680  0.156894106         0.10147048       0.226595532         0.24435622
## Lag 1638400 0.007637041        -0.04655592      -0.007443898        -0.07226516
##                 mutual gwesp.OTP.fixed.0.5 gwdsp.OTP.fixed.0.5
## Lag 0       0.69025542         0.795564260          0.82655175
## Lag 32768   0.58418987         0.623959752          0.52242442
## Lag 163840  0.42435250         0.432709863          0.35047668
## Lag 327680  0.11948613         0.174673754          0.13223947
## Lag 1638400 0.05123385         0.007771714         -0.02509792
## 
## , , nodematch.female1
## 
##                  edges nodematch.hispanic nodematch.female1 nodematch.eversmk1
## Lag 0       0.90035143        0.796948280        1.00000000         0.79308088
## Lag 32768   0.60258009        0.536790742        0.73348572         0.56527326
## Lag 163840  0.32695326        0.324827911        0.37903351         0.38465484
## Lag 327680  0.11123941        0.111356563        0.21164986         0.27852000
## Lag 1638400 0.07516871       -0.002982911        0.09513563        -0.06106261
##                 mutual gwesp.OTP.fixed.0.5 gwdsp.OTP.fixed.0.5
## Lag 0       0.79999770          0.88951827          0.87107087
## Lag 32768   0.66026068          0.69041074          0.56750224
## Lag 163840  0.38096094          0.39655308          0.32909183
## Lag 327680  0.07195343          0.12801382          0.08708550
## Lag 1638400 0.11308394          0.09505784          0.04044172
## 
## , , nodematch.eversmk1
## 
##                   edges nodematch.hispanic nodematch.female1 nodematch.eversmk1
## Lag 0        0.84731435          0.7724498        0.79308088          1.0000000
## Lag 32768    0.54365021          0.5122084        0.63731624          0.6624233
## Lag 163840   0.31661036          0.3735145        0.38613833          0.4631210
## Lag 327680   0.12487907          0.1838576        0.21306300          0.2895293
## Lag 1638400 -0.04843904         -0.0871528       -0.05860075         -0.1732522
##                  mutual gwesp.OTP.fixed.0.5 gwdsp.OTP.fixed.0.5
## Lag 0        0.73949417          0.82596806          0.82962588
## Lag 32768    0.59917271          0.64206417          0.53636921
## Lag 163840   0.36156912          0.38961111          0.32502461
## Lag 327680   0.06513275          0.10756201          0.12157020
## Lag 1638400 -0.02126220         -0.05784788         -0.05300152
## 
## , , mutual
## 
##                   edges nodematch.hispanic nodematch.female1 nodematch.eversmk1
## Lag 0       0.832969818          0.6902554        0.79999770         0.73949417
## Lag 32768   0.655957685          0.5420351        0.68082349         0.60650896
## Lag 163840  0.453711697          0.3807566        0.46832909         0.47654529
## Lag 327680  0.189592365          0.1950812        0.25444882         0.34592646
## Lag 1638400 0.004326463         -0.0397559        0.03453263        -0.04956656
##                 mutual gwesp.OTP.fixed.0.5 gwdsp.OTP.fixed.0.5
## Lag 0       1.00000000          0.91166903         0.790126039
## Lag 32768   0.77089766          0.75016262         0.613992396
## Lag 163840  0.51073753          0.53492576         0.445401161
## Lag 327680  0.19116258          0.22568907         0.144338541
## Lag 1638400 0.01557354          0.02072621        -0.002615637
## 
## , , gwesp.OTP.fixed.0.5
## 
##                  edges nodematch.hispanic nodematch.female1 nodematch.eversmk1
## Lag 0       0.91366631         0.79556426        0.88951827         0.82596806
## Lag 32768   0.65221015         0.57748172        0.71103822         0.63534710
## Lag 163840  0.40355191         0.36375124        0.42906065         0.45848417
## Lag 327680  0.16182896         0.15751100        0.23871746         0.30543634
## Lag 1638400 0.02774368        -0.01550744        0.04360474        -0.05912761
##                 mutual gwesp.OTP.fixed.0.5 gwdsp.OTP.fixed.0.5
## Lag 0       0.91166903          1.00000000          0.88286005
## Lag 32768   0.75714027          0.74743488          0.62020864
## Lag 163840  0.47254922          0.48618158          0.40054594
## Lag 327680  0.14530942          0.18887509          0.12356707
## Lag 1638400 0.05355936          0.04005611          0.01544559
## 
## , , gwdsp.OTP.fixed.0.5
## 
##                  edges nodematch.hispanic nodematch.female1 nodematch.eversmk1
## Lag 0       0.97089215         0.82655175        0.87107087         0.82962588
## Lag 32768   0.56904543         0.49933571        0.63747170         0.51566990
## Lag 163840  0.31817376         0.32249022        0.37414872         0.32999678
## Lag 327680  0.15987338         0.11941690        0.21123819         0.24152798
## Lag 1638400 0.01040193        -0.02676337        0.01558998        -0.05445063
##                 mutual gwesp.OTP.fixed.0.5 gwdsp.OTP.fixed.0.5
## Lag 0       0.79012604           0.8828601          1.00000000
## Lag 32768   0.64720629           0.6437981          0.56197239
## Lag 163840  0.40245842           0.4041699          0.32130564
## Lag 327680  0.09213271           0.1437246          0.12697167
## Lag 1638400 0.06161009           0.0289774         -0.01011366
  1. Geweke Diagnostic: From the function’s help file:

“If the samples are drawn from the stationary distribution of the chain, the two means are equal and Geweke’s statistic has an asymptotically standard normal distribution. […] The Z-score is calculated under the assumption that the two parts of the chain are asymptotically independent, which requires that the sum of frac1 and frac2 be strictly less than 1.””

—?coda::geweke.diag

Let’s take a look at a single chain:

coda::geweke.diag(sample_uncentered)[[1]]
## 
## Fraction in 1st window = 0.1
## Fraction in 2nd window = 0.5 
## 
##               edges  nodematch.hispanic   nodematch.female1  nodematch.eversmk1 
##             -1.0828             -0.9888             -1.7401             -0.8217 
##              mutual gwesp.OTP.fixed.0.5 gwdsp.OTP.fixed.0.5 
##             -1.4265             -1.1219             -0.8655
  1. (not included) Gelman Diagnostic: From the function’s help file:

Gelman and Rubin (1992) propose a general approach to monitoring convergence of MCMC output in which m > 1 parallel chains are run with starting values that are overdispersed relative to the posterior distribution. Convergence is diagnosed when the chains have ‘forgotten’ their initial values, and the output from all chains is indistinguishable. The gelman.diag diagnostic is applied to a single variable from the chain. It is based a comparison of within-chain and between-chain variances, and is similar to a classical analysis of variance. —?coda::gelman.diag

As a difference from the previous diagnostic statistic, this uses all chains simultaneously:

coda::gelman.diag(sample_uncentered)
## Potential scale reduction factors:
## 
##                     Point est. Upper C.I.
## edges                     1.05       1.14
## nodematch.hispanic        1.02       1.04
## nodematch.female1         1.07       1.20
## nodematch.eversmk1        1.07       1.22
## mutual                    1.07       1.20
## gwesp.OTP.fixed.0.5       1.09       1.26
## gwdsp.OTP.fixed.0.5       1.06       1.18
## 
## Multivariate psrf
## 
## 1.15

As a rule of thumb, values in the [.9,1.1] are good.

One nice feature of the mcmc.diagnostics function is the nice trace and posterior distribution plots that it generates. If you have the R package latticeExtra (Sarkar and Andrews 2022), the function will override the default plots used by coda::plot.mcmc and use lattice instead, creating nicer-looking plots. The next code chunk calls the mcmc.diagnostic function, but we suppress the rest of the output (see figure ?fig-coda-plots).

# [2022-03-13] This line is failing for what it could be an ergm bug
# mcmc.diagnostics(ans0, center = FALSE) # Suppressing all the output

If we call the function mcmc.diagnostics, this message appears at the end:

MCMC diagnostics shown here are from the last round of simulation, prior to computation of final parameter estimates. Because the final estimates are refinements of those used for this simulation run, these diagnostics may understate model performance. To directly assess the performance of the final model on in-model statistics, please use the GOF command: gof(ergmFitObject, GOF=~model).

—mcmc.diagnostics(ans0)

Not that bad (although the mutual term could do better)!3 First, observe that in the figure, we see four different lines; why is that? Since we were running in parallel using four cores, the algorithm ran four chains of the MCMC algorithm. An eyeball test is to see if all the chains moved at about the same place; in such a case, we can start thinking about model convergence from the MCMC perspective.

Once we are sure to have reach convergence on the MCMC algorithm, we can start thinking about how well does our model predicts the observed network’s proterties. Besides the statistics that define our ERGM, the gof function’s default behavior show GOF for:

  1. In degree distribution,
  2. Out degree distribution,
  3. Edge-wise shared partners, and
  4. Geodesics

Let’s take a look at it

# Computing and printing GOF estatistics
ans_gof <- gof(ans2)
ans_gof
## 
## Goodness-of-fit for in-degree 
## 
##           obs min  mean max MC p-value
## idegree0   13   1  6.36  12       0.00
## idegree1   34  12 20.37  30       0.00
## idegree2   37  21 34.82  51       0.80
## idegree3   48  30 46.34  66       0.82
## idegree4   37  38 52.81  67       0.00
## idegree5   47  42 54.17  72       0.36
## idegree6   42  34 48.49  66       0.44
## idegree7   39  21 41.75  59       0.70
## idegree8   35  15 34.14  51       0.86
## idegree9   21  14 25.98  38       0.44
## idegree10  12   9 19.11  35       0.12
## idegree11  19   4 13.15  21       0.14
## idegree12   4   3  8.53  16       0.12
## idegree13   7   1  5.25  11       0.58
## idegree14   6   0  3.31   8       0.18
## idegree15   3   0  1.67   6       0.48
## idegree16   4   0  0.82   6       0.06
## idegree17   3   0  0.53   4       0.04
## idegree18   3   0  0.26   2       0.00
## idegree19   2   0  0.10   2       0.02
## idegree20   1   0  0.04   2       0.06
## idegree22   1   0  0.00   0       0.00
## 
## Goodness-of-fit for out-degree 
## 
##           obs min  mean max MC p-value
## odegree0    4   2  6.90  14       0.26
## odegree1   28  10 19.15  30       0.06
## odegree2   45  23 32.45  46       0.02
## odegree3   50  27 44.37  60       0.40
## odegree4   54  34 52.97  71       0.96
## odegree5   62  38 53.24  72       0.18
## odegree6   40  39 51.80  75       0.02
## odegree7   28  32 45.95  61       0.00
## odegree8   13  22 34.51  52       0.00
## odegree9   16  17 27.64  39       0.00
## odegree10  20  11 19.13  28       0.92
## odegree11   8   2 12.76  20       0.18
## odegree12  11   2  8.08  14       0.42
## odegree13  13   0  4.18  10       0.00
## odegree14   6   0  2.49   7       0.06
## odegree15   6   0  1.15   4       0.00
## odegree16   7   0  0.68   4       0.00
## odegree17   4   0  0.22   3       0.00
## odegree18   3   0  0.15   1       0.00
## odegree19   0   0  0.06   1       1.00
## odegree20   0   0  0.10   2       1.00
## odegree22   0   0  0.01   1       1.00
## odegree23   0   0  0.01   1       1.00
## 
## Goodness-of-fit for edgewise shared partner 
## 
##           obs min    mean  max MC p-value
## esp.OTP0 1032 991 1046.85 1114       0.60
## esp.OTP1  755 777  830.99  905       0.00
## esp.OTP2  352 288  355.30  414       0.78
## esp.OTP3  202 101  122.85  148       0.00
## esp.OTP4   79  25   39.83   54       0.00
## esp.OTP5   36   3    9.82   26       0.00
## esp.OTP6   14   0    2.26    9       0.00
## esp.OTP7    4   0    0.53    2       0.00
## esp.OTP8    1   0    0.08    1       0.16
## 
## Goodness-of-fit for minimum geodesic distance 
## 
##       obs   min     mean   max MC p-value
## 1    2475  2308  2408.51  2618       0.10
## 2   10672  9717 10526.74 12093       0.62
## 3   31134 32726 36472.28 42060       0.00
## 4   50673 62083 66619.95 71128       0.00
## 5   42563 36051 41272.32 45938       0.44
## 6   18719  6165  9506.31 14061       0.00
## 7    4808   481  1321.87  2588       0.00
## 8     822    11   143.17   505       0.00
## 9     100     0    12.69   269       0.02
## 10      7     0     1.21    84       0.02
## 11      0     0     0.13    12       1.00
## Inf 12333  2904  6020.82 11478       0.00
## 
## Goodness-of-fit for model statistics 
## 
##                           obs       min      mean       max MC p-value
## edges                2475.000  2308.000  2408.510  2618.000       0.10
## nodematch.hispanic   1832.000  1667.000  1758.880  1860.000       0.08
## nodematch.female1    1879.000  1696.000  1771.860  1957.000       0.04
## nodematch.eversmk1   1755.000  1604.000  1702.570  1880.000       0.24
## mutual                486.000   428.000   448.360   465.000       0.00
## gwesp.OTP.fixed.0.5  1775.406  1506.382  1601.146  1792.351       0.02
## gwdsp.OTP.fixed.0.5 13187.633 11655.503 12574.732 14495.043       0.12

# Plotting GOF statistics
plot(ans_gof)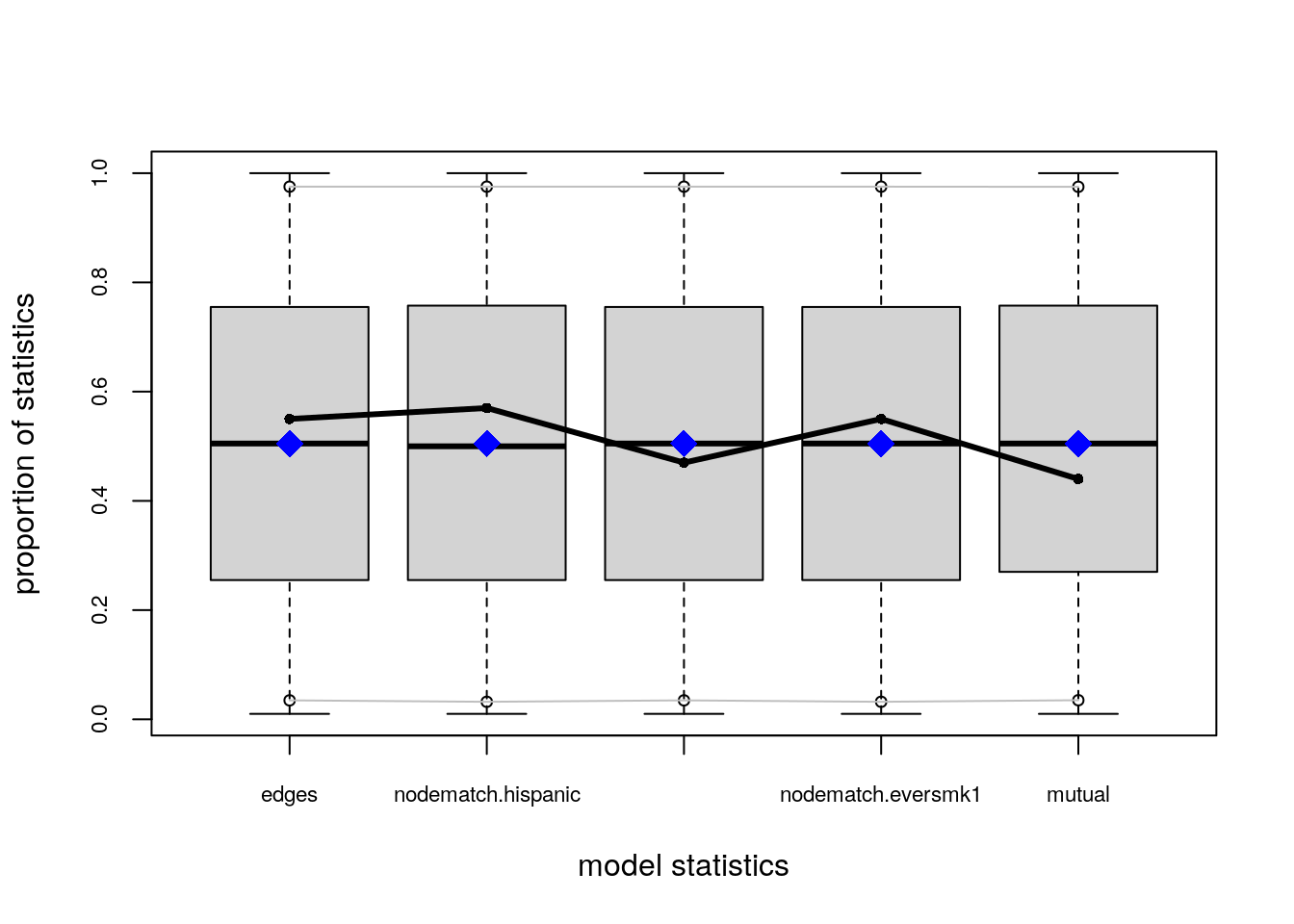

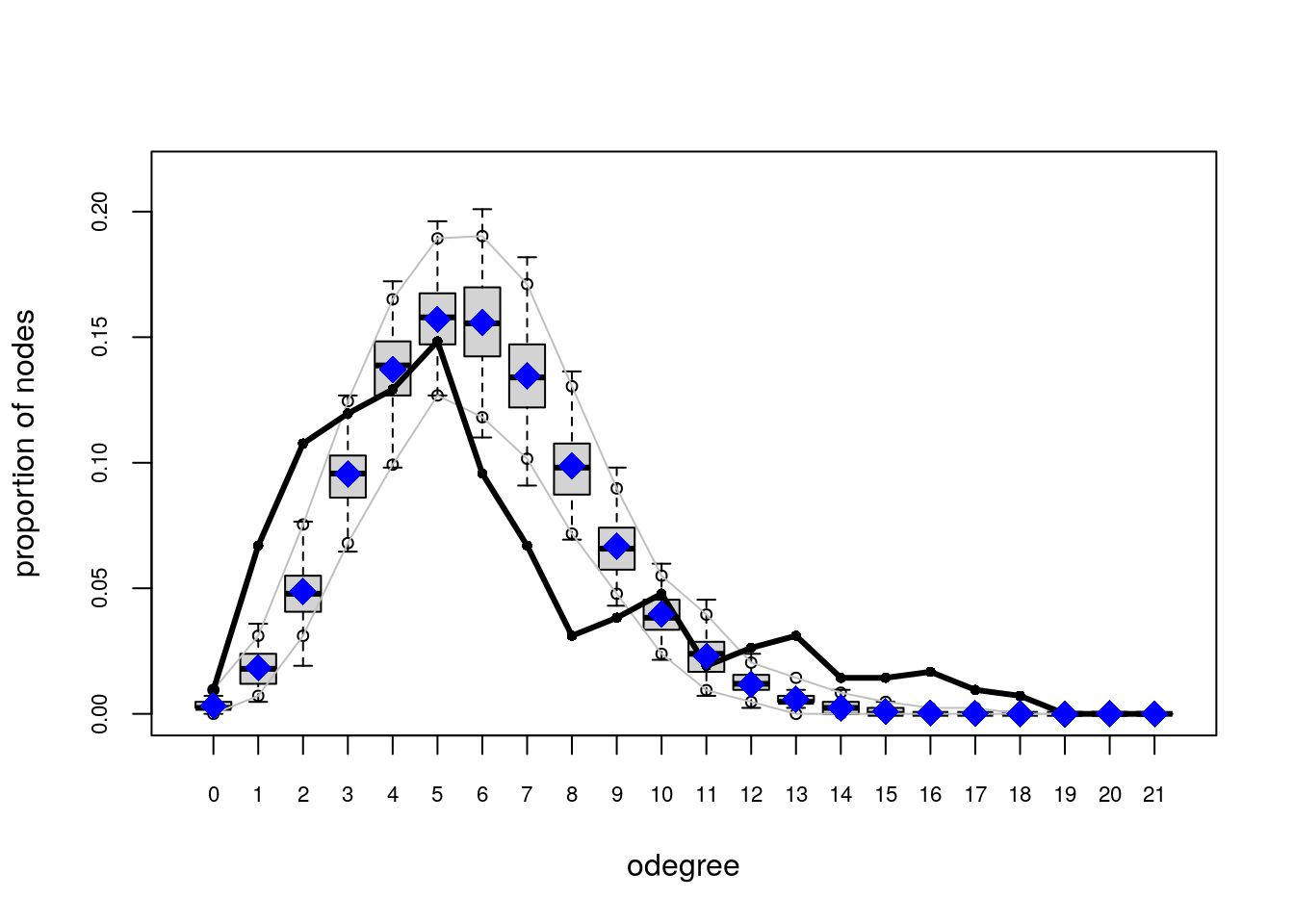
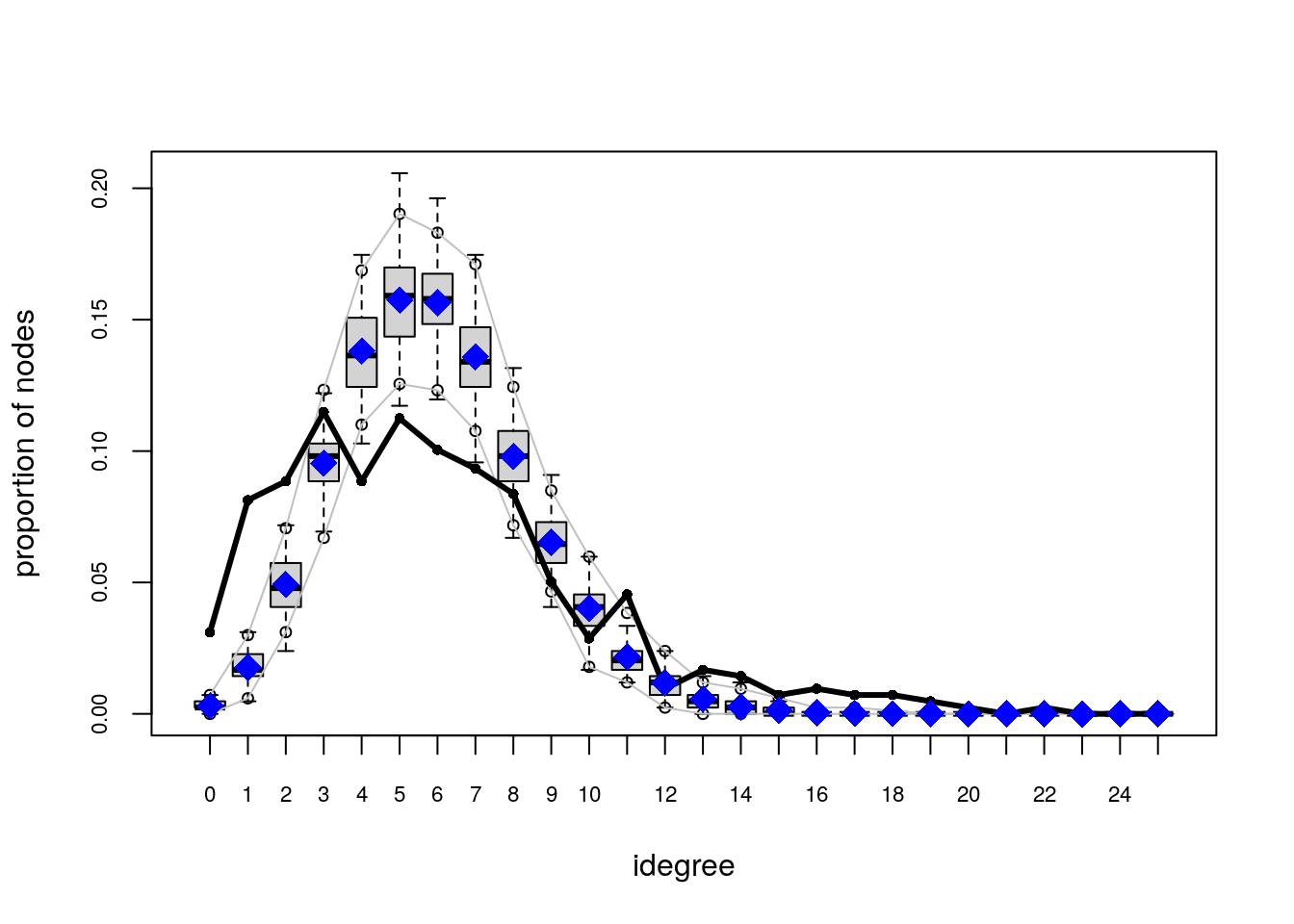
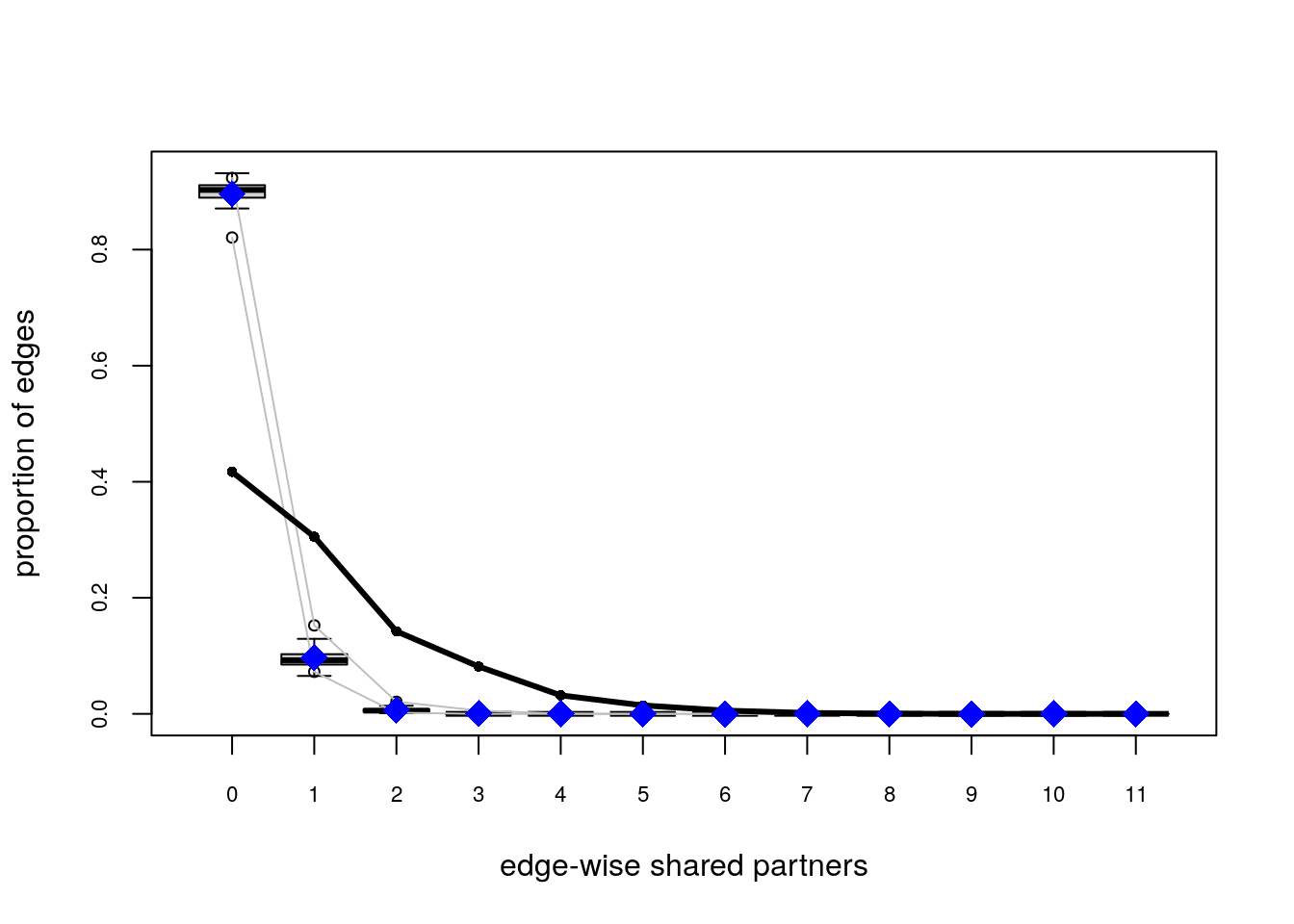
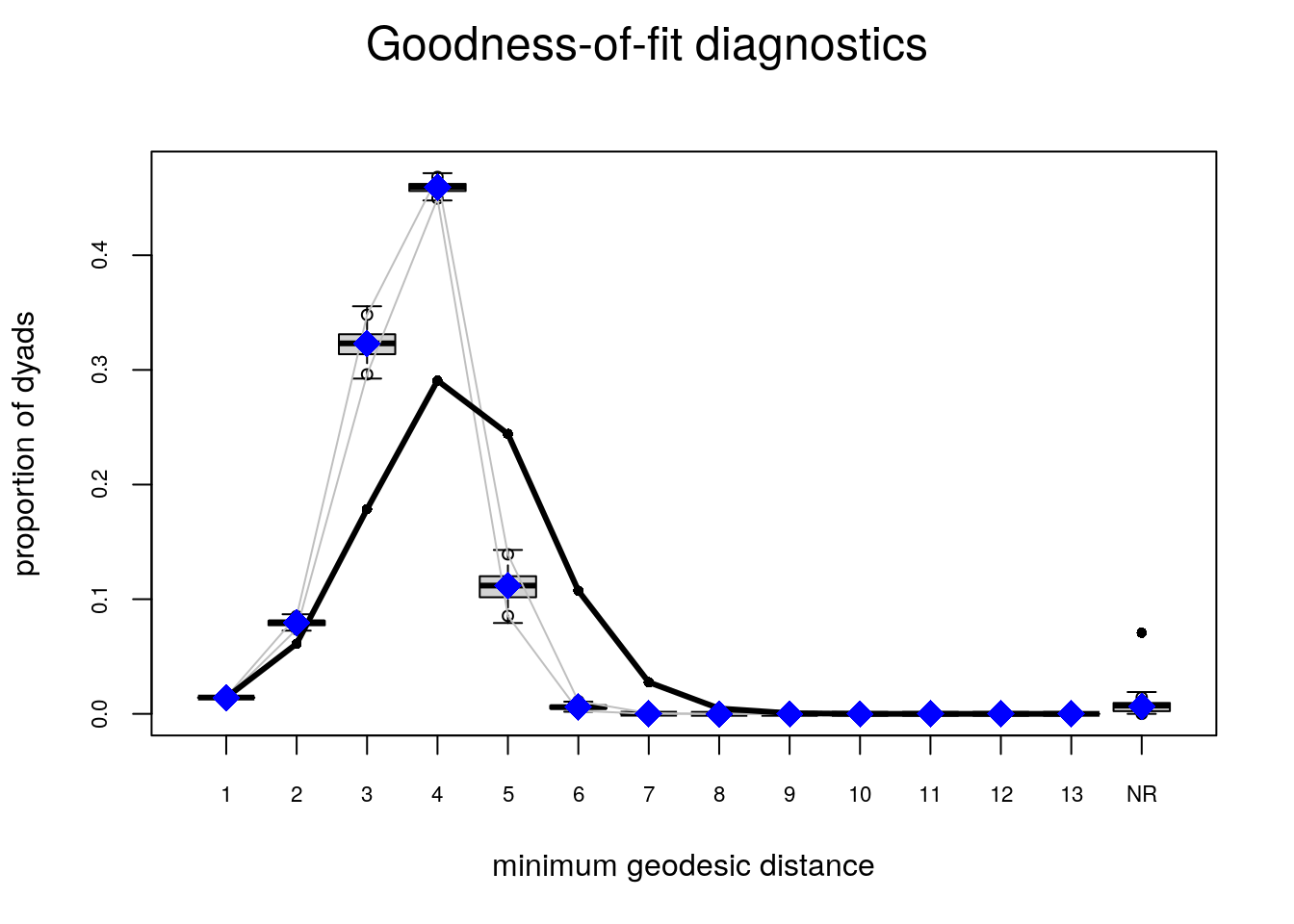
Try the following configuration instead

ans0_bis <- ergm(
  network_111 ~
    edges +
    nodematch("hispanic") +
    nodematch("female1") +
    mutual + 
    esp(0:3) + 
    idegree(0:10)
    ,
  control = control.ergm(
    seed        = 1,
    MCMLE.maxit = 15,
    parallel    = 4,
    CD.maxit    = 15,
    MCMC.samplesize = 2048*4,
    MCMC.burnin = 30000,
    MCMC.interval = 2048*4
    )
  )

Increase the sample size, so the curves are smoother, longer intervals (thinning), which reduces autocorrelation, and a larger burin. All this together to improve the Gelman test statistic. We also added idegree from 0 to 10, and esp from 0 to 3 to explicitly match those statistics in our model.

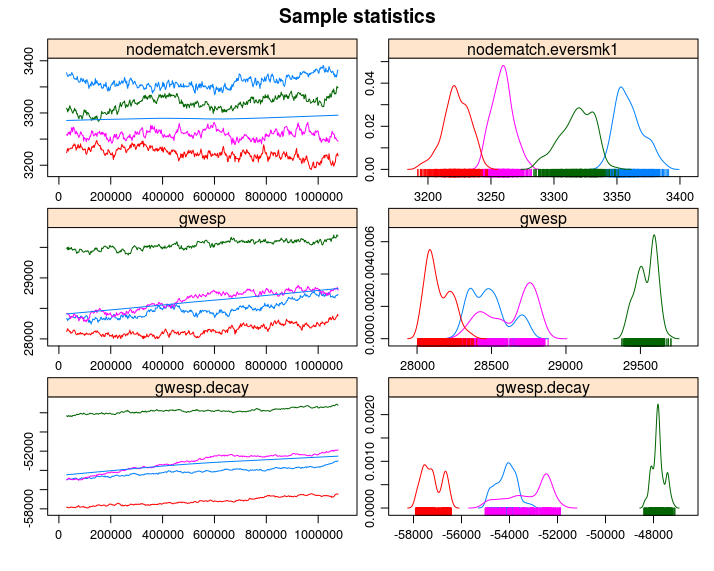
An example of a terrible ERGM (no convergence at all). Also, a good example of why running multiple chains can be useful

More on MCMC convergence

For more on this issue, I recommend reviewing chapter 1 and chapter 6 from the Handbook of MCMC (Brooks et al. 2011). Both chapters are free to download from the book’s website.

For GOF take a look at section 6 of ERGM 2016 Sunbelt tutorial, and for a more technical review, you can take a look at (David R. Hunter, Goodreau, and Handcock 2008).

Mathematical Interpretation

One of the most critical parts of statistical modeling is interpreting the results, if not the most important. In the case of ERGMs, a key aspect is based on change statistics. Suppose that we would like to know how likely the tie y_{ij} is to happen, given the rest of the network. We can compute such probabilities using what literature sometimes describes as the Gibbs-sampler.

In particular, the log-odds of the ij tie ocurring conditional on the rest of the network can be written as:

\begin{equation} \text{logit}\left({\Pr{y_{ij} = 1|y_{-ij}}}\right) = {\theta}^\mathbf{t}\Delta\delta\left(y_{ij}:0\to 1\right), \end{equation}

with \delta\left(y_{ij}:0\to 1\right)\equiv s\left(\mathbf{y}\right)_{\text{ij}}^+ - s\left(\mathbf{y}\right)_{\text{ij}}^- as the vector of change statistics, in other words, the difference between the sufficient statistics when y_{ij}=1 and its value when y_{ij} = 0. To show this, we write the following:

\begin{align*} \Pr{y_{ij} = 1|y_{-ij}} & = % \frac{\Pr{y_{ij} = 1, x_{-ij}}}{% {\mathbb{P}_{+}\left(y_{ij} = 1, y_{-ij}\right) } \Pr{y_{ij} = 0, y_{-ij}}} \\ & = \frac{\text{exp}\left\{{\theta}^\mathbf{t}s\left(\mathbf{y}\right)^+_{ij}\right\}}{% \text{exp}\left\{{\theta}^\mathbf{t}s\left(\mathbf{y}\right)^+_{ij}\right\} + \text{exp}\left\{{\theta}^\mathbf{t}s\left(\mathbf{y}\right)^-_{ij}\right\}} \end{align*}

Applying the logit function to the previous equation, we obtain:

\begin{align*} & = \text{log}\left\{\frac{\text{exp}\left\{{\theta}^\mathbf{t}s\left(\mathbf{y}\right)^+_{ij}\right\}}{% \text{exp}\left\{{\theta}^\mathbf{t}s\left(\mathbf{y}\right)^+_{ij}\right\} + % \text{exp}\left\{{\theta}^\mathbf{t}s\left(\mathbf{y}\right)^-_{ij}\right\}}\right\} - % \text{log}\left\{ % \frac{\text{exp}\left\{{\theta}^\mathbf{t}s\left(\mathbf{y}\right)^-_{ij}\right\}}{% \text{exp}\left\{{\theta}^\mathbf{t}s\left(\mathbf{y}\right)^+_{ij}\right\} + \text{exp}\left\{{\theta}^\mathbf{t}s\left(\mathbf{y}\right)^-_{ij}\right\}}% \right\} \\ & = \text{log}\left\{\text{exp}\left\{{\theta}^\mathbf{t}s\left(\mathbf{y}\right)^+_{ij}\right\}\right\} - \text{log}\left\{\text{exp}\left\{{\theta}^\mathbf{t}s\left(\mathbf{y}\right)^-_{ij}\right\}\right\} \\ & = {\theta}^\mathbf{t}\left(s\left(\mathbf{y}\right)^+_{ij} - s\left(\mathbf{y}\right)^-_{ij}\right) \\ & = {\theta}^\mathbf{t}\Delta\delta\left(y_{ij}:0\to 1\right) \end{align*} Henceforth, the conditional probability of node n gaining function k can be written as:

\begin{equation} {\mathbb{P}_{=}\left(y_{ij} = 1|y_{-ij}\right) } \frac{1}{1 + \text{exp}\left\{-{\theta}^\mathbf{t}\Delta\delta\left(y_{ij}:0\to 1\right)\right\}} \end{equation}

i.e., a logistic probability.

Markov independence

The challenge of analyzing networks is their interdependent nature. Nonetheless, in the absence of such interdependence, ERGMs are equivalent to logistic regression. Conceptually, if all the statistics included in the model do not involve two or more dyads, then the model is non-Markovian in the sense of Markov graphs.

Mathematically, to see this, it suffices to show that the ERGM probability can be written as the product of each dyads’ probabilities.

\begin{equation*} {\mathbb{P}_{=}\left(\mathbf{y} | \theta\right) } \frac{\text{exp}\left\{{\theta}^\mathbf{t}s\left(\mathbf{y}\right)\right\}}{\sum_{y}\text{exp}\left\{{\theta}^\mathbf{t}s\left(\mathbf{y}\right)\right\}} = \frac{\prod_{ij}\text{exp}\left\{{\theta}^\mathbf{t}s\left(\mathbf{y}\right)_{ij}\right\}}{\sum_{y}\text{exp}\left\{{\theta}^\mathbf{t}s\left(\mathbf{y}\right)\right\}} \end{equation*}

Where s\left(\right)_{ij} is a function such that s\left(\mathbf{y}\right) = \sum_{ij}{s\left(\mathbf{y}\right)_{ij}}. We now need to deal with the normalizing constant. To see how that can be saparated, let’s start from the result:

\begin{align*} & =\prod_{ij}\left(1 + \text{exp}\left\{{\theta}^\mathbf{t}s\left(\mathbf{y}\right)_{ij}\right\}\right) \\ & = \left(1 + \text{exp}\left\{{\theta}^\mathbf{t}s\left(\mathbf{y}\right)_{11}\right\}\right)\left(1 + \text{exp}\left\{{\theta}^\mathbf{t}s\left(\mathbf{y}\right)_{12}\right\}\right)\dots\left(1 + \text{exp}\left\{{\theta}^\mathbf{t}s\left(\mathbf{y}\right)_{nn}\right\}\right) \\ & = 1 + \text{exp}\left\{{\theta}^\mathbf{t}s\left(\mathbf{y}\right)_{11}\right\} + \text{exp}\left\{{\theta}^\mathbf{t}s\left(\mathbf{y}\right)_{11}\right\}\text{exp}\left\{{\theta}^\mathbf{t}s\left(\mathbf{y}\right)_{12}\right\} + \dots + \prod_{ij}\text{exp}\left\{{\theta}^\mathbf{t}s\left(\mathbf{y}\right)_{ij}\right\} \\ & = 1 + \text{exp}\left\{{\theta}^\mathbf{t}s\left(\mathbf{y}\right)_{11}\right\} + \text{exp}\left\{{\theta}^\mathbf{t}\left(s\left(\mathbf{y}\right)_{11} + s\left(\mathbf{y}\right)_{12}\right)\right\} + \dots + \prod_{ij}\text{exp}\left\{{\theta}^\mathbf{t}s\left(\mathbf{y}\right)_{ij}\right\} \\ & = \sum_{\mathbf{y}\in\mathcal{Y}}\text{exp}\left\{{\theta}^\mathbf{t}s\left(\mathbf{y}\right)\right\} \end{align*}

Where the last equality follows from the fact that the sum is the sum over all possible combinations of networks, starting from exp(0) = 1, up to exp(all). This way, we can now write:

\begin{equation} \frac{\prod_{ij}\text{exp}\left\{{\theta}^\mathbf{t}s\left(\mathbf{y}\right)_{ij}\right\}}{\sum_{y}\text{exp}\left\{{\theta}^\mathbf{t}s\left(\mathbf{y}\right)\right\}} = \prod_{ij}\frac{\text{exp}\left\{{\theta}^\mathbf{t}s\left(\mathbf{y}\right)_{ij}\right\}}{1 + \text{exp}\left\{{\theta}^\mathbf{t}s\left(\mathbf{y}\right)_{ij}\right\}} \end{equation}

Related to this, block-diagonal ERGMs can be estimated as independent models, one per block. To see more about this, read (SNIJDERS 2010). Likewise, since independence depends–pun intended–on partitioning the objective function, as pointed by Snijders, non-linear functions make the model dependent, e.g., s\left(\mathbf{y}\right) = \sqrt{\sum_{ij}y_{ij}}, the square root of the edgecount is no longer a bernoulli graph.

  1. You can download the 03.rda file from this link.↩︎

  2. Yes, the classes have the same name as the packages.↩︎

  3. The statnet wiki website as a very nice example of (very) bad and good MCMC diagnostics plots here.↩︎